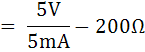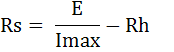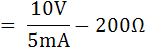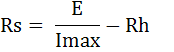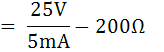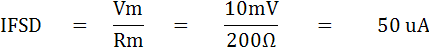3.2.1 โวลท์มิเตอร์กระแสสลับแบบครึ่งคลื่น (Half wave Rectifier) โดยการนำไดโอดมาทำการเรียงกระแสแบบครึ่งคลื่นดังรูปที่ 3.2
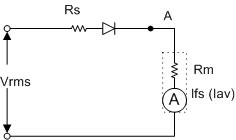 รูปที่ 3.2 แสดงวงจรโวลท์มิเตอร์กระแสสลับแบบ Half wave Rectifier
จากรูปที่ 3.2 ค่ากระแสที่จุด A (ที่จะผ่านมิเตอร์มูฟเม้นท์) จะเป็นลักษณะแบบครึ่งคลื่น ซึ่งคิดเป็นกระแสเฉลี่ยคือ
รูปที่ 3.2 แสดงวงจรโวลท์มิเตอร์กระแสสลับแบบ Half wave Rectifier
จากรูปที่ 3.2 ค่ากระแสที่จุด A (ที่จะผ่านมิเตอร์มูฟเม้นท์) จะเป็นลักษณะแบบครึ่งคลื่น ซึ่งคิดเป็นกระแสเฉลี่ยคือ
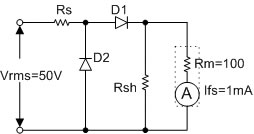
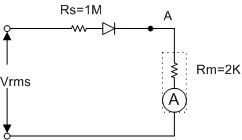 จากรูปจงหาค่า Vrms ที่ทำให้เข็มมิเตอร์ชี้เต็มสเกล และถ้าต้องการวัดค่า Vrms เท่ากับ 50V พอดี จะต้องใช้ค่าความต้านทานเท่าไร
จากรูปจงหาค่า Vrms ที่ทำให้เข็มมิเตอร์ชี้เต็มสเกล และถ้าต้องการวัดค่า Vrms เท่ากับ 50V พอดี จะต้องใช้ค่าความต้านทานเท่าไร
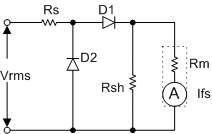 รูปที่ 3.3 แสดงวงจร Ac Voltmeter แบบ Half wave rectifier ในทางปฏิบัติ
จากรูปที่ 3.3 ถ้าเรากำหนดให้ Rsh เท่ากับค่าความต้านทานภายในของมิเตอร์มูฟเม้นท์ จะทำให้กระแสที่ไหลผ่านไดโอดสูงขึ้นเป็น 2 เท่า เนื่องจากความต้านทานที่เป็น
โหลดของวงจรลดลงครึ่งหนึ่งนั่นเอง ดังนั้นสมการในการคำนวณค่า Rs และค่าความไว จะเขียนได้ใหม่ดังนี้
รูปที่ 3.3 แสดงวงจร Ac Voltmeter แบบ Half wave rectifier ในทางปฏิบัติ
จากรูปที่ 3.3 ถ้าเรากำหนดให้ Rsh เท่ากับค่าความต้านทานภายในของมิเตอร์มูฟเม้นท์ จะทำให้กระแสที่ไหลผ่านไดโอดสูงขึ้นเป็น 2 เท่า เนื่องจากความต้านทานที่เป็น
โหลดของวงจรลดลงครึ่งหนึ่งนั่นเอง ดังนั้นสมการในการคำนวณค่า Rs และค่าความไว จะเขียนได้ใหม่ดังนี้
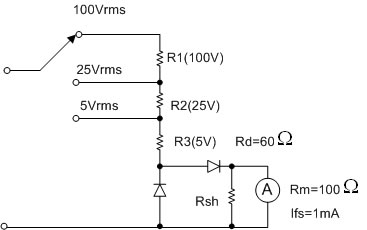
ตัวอย่างที่ 4 จงออกแบบวงจร AC Voltmeter แบบ Half wave rectifier 3 ย่านวัด คือ 5Vrms, 25Vrms และ 100Vrms จากมิเตอร์ มูฟเม้นท์ขนาด 1mA, 100W
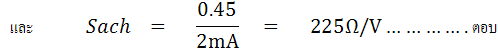
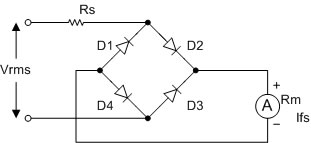 รูปที่ 3.4 แสดงวงจรโวลท์มิเตอร์กระแสสลับแบบ Full wave Rectifier
จากรูปที่ 3.4 ค่ากระแสที่ไหลผ่านมิเตอร์มูฟเม้นท์ จะเป็นลักษณะแบบเต็มคลื่น คิดเป็นกระแสเฉลี่ยได้เป็น 2 เท่าของวงจร Half wave คือ
รูปที่ 3.4 แสดงวงจรโวลท์มิเตอร์กระแสสลับแบบ Full wave Rectifier
จากรูปที่ 3.4 ค่ากระแสที่ไหลผ่านมิเตอร์มูฟเม้นท์ จะเป็นลักษณะแบบเต็มคลื่น คิดเป็นกระแสเฉลี่ยได้เป็น 2 เท่าของวงจร Half wave คือ
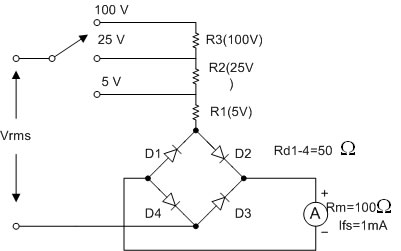 หาความต้านทานรวมในแต่ละย่าน (Rin)
หาความต้านทานรวมในแต่ละย่าน (Rin)
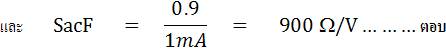 3.3 ผลการโหลดของ AC Voltmeter
3.3 ผลการโหลดของ AC VoltmeterAC Voltmeter ไม่ว่าจะเป็นแบบชนิด Half wave rectifier หรือ Full wave rectifier จะมีความไวน้อยกว่า DC Voltmeter ดังนั้นการโหลดของ AC Voltmeter จึงมีมากกว่า DC Voltmeter หรือความถูกต้อง (Accuracy) ของ DC Voltmeter จะมีมากกว่า AC Voltmeter ดังตัวอย่างที่ 7
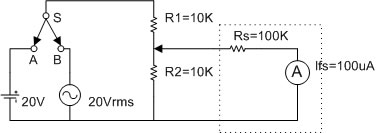
ตัวอย่างที่ 7) DC Voltmeter มี Sensitivity = 20 KW / V
AC Voltmeter มี Sensitivity = 5 KW / V
จงคำนวณหาความต้านทานภายในที่ย่านวัด 10Vdc และ 10Vrms ย่านวัด 10 Vdc
 DC Voltmeter
DC Voltmeter
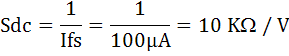
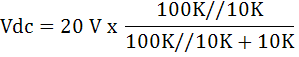
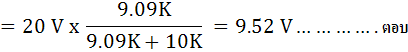 AC Voltmeter (Have wave)
AC Voltmeter (Have wave)
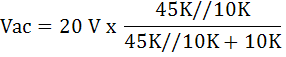
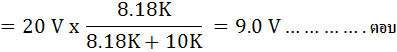 AC Voltmeter (Full wave)
AC Voltmeter (Full wave)
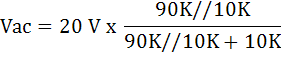
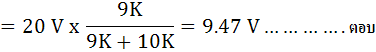 เพราะฉะนั้นจะเห็นว่า AC Voltmeter ไม่ว่าจะเป็น Half wave หรือ Full wave rectifier ก็ตามจะมีการโหลดมากกว่า DC Voltmeter
3.4 การปรับเทียบสเกลของเครื่องวัดแบบเรียงกระแส
โดยปกติจะปรับเทียบสเกลของเครื่องวัดแบบเรียงกระแสให้อ่านค่าแรงดันเป็นค่าประสิทธิผล (rms) (กรณีกระแสที่ผ่านไปยังส่วนเคลื่อนที่เป็นรูปซายน์ที่ถูกเรียงกระ
แสอย่างไม่ผิดเพี้ยน) เนื่องจากส่วนเคลื่อนที่ตอบสนองต่อค่าเฉลี่ยแต่ต้องการปรับเทียบเป็นค่าประสิทธิผล ดังนั้นจึงจะต้องมีค่าฟอร์มแฟกเตอร์ (form factor) มาเกี่ยวข้องในการทำ
สเกล จะต้องสัมพันธ์กับมุมที่ส่วนเคลื่อนที่เบี่ยงเบนไป โดยสำหรับโวลท์มิเตอร์แบบเรียงกระแสเต็มคลื่น ค่าที่อ่านได้จากเครื่องวัดคือ
เพราะฉะนั้นจะเห็นว่า AC Voltmeter ไม่ว่าจะเป็น Half wave หรือ Full wave rectifier ก็ตามจะมีการโหลดมากกว่า DC Voltmeter
3.4 การปรับเทียบสเกลของเครื่องวัดแบบเรียงกระแส
โดยปกติจะปรับเทียบสเกลของเครื่องวัดแบบเรียงกระแสให้อ่านค่าแรงดันเป็นค่าประสิทธิผล (rms) (กรณีกระแสที่ผ่านไปยังส่วนเคลื่อนที่เป็นรูปซายน์ที่ถูกเรียงกระ
แสอย่างไม่ผิดเพี้ยน) เนื่องจากส่วนเคลื่อนที่ตอบสนองต่อค่าเฉลี่ยแต่ต้องการปรับเทียบเป็นค่าประสิทธิผล ดังนั้นจึงจะต้องมีค่าฟอร์มแฟกเตอร์ (form factor) มาเกี่ยวข้องในการทำ
สเกล จะต้องสัมพันธ์กับมุมที่ส่วนเคลื่อนที่เบี่ยงเบนไป โดยสำหรับโวลท์มิเตอร์แบบเรียงกระแสเต็มคลื่น ค่าที่อ่านได้จากเครื่องวัดคือ
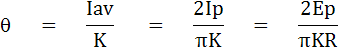 เมื่อแทนค่า q ในสมการแรงดัน จะได้
เมื่อแทนค่า q ในสมการแรงดัน จะได้
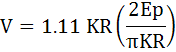
สเกลโวลท์มิเตอร์ที่ใช้เรียงกระแสแบบบริดจ์ จะมีลักษณะสม่ำเสมอ (Uniform) เนื่องจากความต้านทานที่นำมาต่อมีค่าสูง เมื่อเทียบกับความต้านทานของไดโอดทำให้มุมที่ เข็มเบี่ยงเบนไปมีค่าคงที่คูณกับค่ายอดของแรงดันที่วัดนั้นส่วนย่านต่ำความต้านทานที่นำมาต่ออนุกรมมีค่าไม่มากนัก เมื่อเทียบกับความต้านทานของไดโอดเมื่อได้รับไบอัสตรงและเนื่อง จากกระที่ไหลต่ำลงด้วย ค่าความต้านทานของไดโอดขณะนี้จึงสูงกว่าขณะเมื่อมีกระแสค่ามากไหลผ่านทำให้การเบี่ยงเบนของเข็มมีค่าน้อย และสเกลจะมีลักษณะไม่สม่ำเสมอ ดังนั้นจึง นิยมแยกสเกลของแรงดันต่ำๆ ไว้ต่างหาก และทำการปรับเทียบไว้โดยเฉพาะ 3.4 อิเล็กโทรไดนาโมมิเตอร์ (Electrodynamometer) อิเล็กโตรไดนาโมมิเตอร์ จะมีลักษณะคล้ายกับมูฟเม้นท์มิเตอร์แบบ ดี-อาร์ซองวาลโดยแทนที่แม่เหล็กถาวรด้วยแม่เหล็กไฟฟ้า (Electromagnet) ซึ่งเป็นขดลวดอยู่กับ ที่ (Fixed coil) แต่แยกเป็นสองส่วน เพื่อให้เกิดสนามแม่เหล็กในบริเวณที่ส่วนขดลวดเคลื่อนที่ (Moving coil) ขดลวดอยู่กับที่ (Fixed coil) จะใช้ลวดขนาดใหญ่เพื่อให้เกิดค่าแอมแปร์- รอบ มากพอที่จะเกิดแรงบิดให้เข็มเบี่ยงเบนได้พอเพียง เรียกขดนี้ว่า ขดกระแส (Current Coil) ส่วนขดลวดที่เคลื่อนที่เรียกว่า ขดแรงดัน (Voltage Coil; Moving Coil) ผลของสนามแม่ เหล็กที่เกิดจากขดลวดกระแสและขดลวดแรงดัน ที่กระทำต่อกัน เมื่อมีกระแสผ่านจะทำให้เกิดแรงบิดเช่นเดียวกับมูฟเม้นท์มิเตอร์แบบ ดี-อาร์ซองวาลแรงบิดนี้จะถูกต้านโดยสปริง ซึ่งใช้ เป็นทางผ่านของกระแสที่เข้าสู่ขดลวดแรงดันด้วย เข็มชี้ที่ติดตั้งบนส่วนเคลื่อนที่ จะแสดงขนาดของปริมาณซึ่งอาจปรับเทียบเป็นค่าโวลท์, แอมแปร์ หรือ วัตต์
อิเล็กโตรไดนาโมมิเตอร์ จะสามารถทนกระแสได้สูงกว่า มูฟเม้นท์มิเตอร์แบบ ดี-อาร์ซองวาล เมื่อไม่มีความต้านทานต่อขนานเพิ่มเข้าไป แต่จะมีความไวต่ำกว่าโดยทั่วไป แล้วจะประมาณ 20 - 100W/V
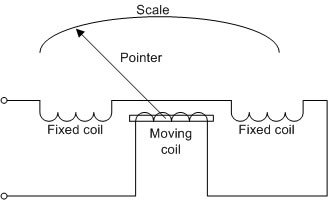 รูปที่ 3.5 แสดงอิเล็กโทรไดนาโมมิเตอร์มูฟเม้นท์
จากรูปที่ 3.5 เป็นลักษณะโครงสร้างของอิเล็กโทรไดนาโมมิเตอร์มูฟเม้นท์ที่นำมาใช้เป็นอิเล็กโทรไดนาโมมิเตอร์ที่ใช้วัดกระแสได้สูงขึ้นโดยการต่อความต้านทาน
ขนานกับส่วนของขดลวดเคลื่อนที่ หรือนำมาวัดแรงดันโดยการต่อความต้านทานอนุกรมเข้าไปนั่นเอง
รูปที่ 3.5 แสดงอิเล็กโทรไดนาโมมิเตอร์มูฟเม้นท์
จากรูปที่ 3.5 เป็นลักษณะโครงสร้างของอิเล็กโทรไดนาโมมิเตอร์มูฟเม้นท์ที่นำมาใช้เป็นอิเล็กโทรไดนาโมมิเตอร์ที่ใช้วัดกระแสได้สูงขึ้นโดยการต่อความต้านทาน
ขนานกับส่วนของขดลวดเคลื่อนที่ หรือนำมาวัดแรงดันโดยการต่อความต้านทานอนุกรมเข้าไปนั่นเอง
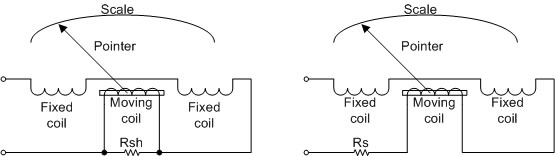 รูปที่ 3.6 แสดงการนำอิเล็กโทรไดนาโมมิเตอร์มาวัดกระแส และแรงดัน
จากรูปที่ 3.6 ก) เป็นการต่อความต้านทานขนานกับ Moving coil เพื่อใช้เป็นแอมมิเตอร์ และจากรูปที่ 3.6 ข) เป็นการต่อความต้านทานอนุกรม (Multiplier) เพื่อ
ใช้เป็นโวลท์มิเตอร์
ตัวอย่างที่ 9) อิเล็กโทรไดนาโมมิเตอร์ตัวหนึ่งมีค่ากระแสที่ทำให้เข็มชี้เต็มสเกล เท่ากับ 10mA นำมาใช้เป็นแอมมิเตอร์สำหรับวัด 1A ถ้าความต้านทานมูฟวิ่งคอยล์เท่า
กับ 40W จงคำนวณหาค่าความต้านทานที่จะนำมาต่อขนานกับ Moving coil นี้การหารค่าความต้านทานจะใช้สมการเดียวกันกับการหาค่า Rsh ในเรื่อง DC Ammeter คือ
รูปที่ 3.6 แสดงการนำอิเล็กโทรไดนาโมมิเตอร์มาวัดกระแส และแรงดัน
จากรูปที่ 3.6 ก) เป็นการต่อความต้านทานขนานกับ Moving coil เพื่อใช้เป็นแอมมิเตอร์ และจากรูปที่ 3.6 ข) เป็นการต่อความต้านทานอนุกรม (Multiplier) เพื่อ
ใช้เป็นโวลท์มิเตอร์
ตัวอย่างที่ 9) อิเล็กโทรไดนาโมมิเตอร์ตัวหนึ่งมีค่ากระแสที่ทำให้เข็มชี้เต็มสเกล เท่ากับ 10mA นำมาใช้เป็นแอมมิเตอร์สำหรับวัด 1A ถ้าความต้านทานมูฟวิ่งคอยล์เท่า
กับ 40W จงคำนวณหาค่าความต้านทานที่จะนำมาต่อขนานกับ Moving coil นี้การหารค่าความต้านทานจะใช้สมการเดียวกันกับการหาค่า Rsh ในเรื่อง DC Ammeter คือ
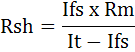
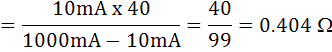
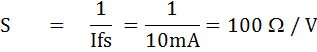
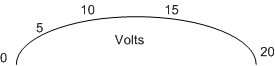 รูปที่ 3.7 แสดงสเกลมิเตอร์แบบกฎกำลังสอง
3.5 ลักษณะจำเพาะของเครื่องวัดแบบอิเล็กโทรไดนาโม
1. สเกลของแอมมิเตอร์และโวลท์มิเตอร์จะมีลักษณะกฎกำลังสอง โดยประมาณ ส่วนสเกลของวัตต์มิเตอร์จะมีลักษณะเป็นเชิงเส้น
2. ต้นทุนในการผลิตสูงกว่า และมีการสูญเสียกำลังสูงกว่าเครื่องวัดแบบ PMMC
3. ใช้วัดค่า rms ของรูปคลื่นกระแสสลับ โดยไม่คำนึงถึงรูปร่างของคลื่น
4. เหมาะสำหรับใช้ทั้งวงจรกระแสตรงและกระแสสลับ โดยไม่ถูกกระทบกระเทือนโดยความถี่บางรุ่นสามารถใช้ในพิสัยความถี่จากกระแสตรงถึง 25 KHz
5. สนามแม่เหล็กรายรอบจะมีผลกระทบต่อการทำงานของเครื่องวัดแบบนี้ ดังนั้นจะต้องวางชุดขดลวดภายในส่วนที่ห่อหุ้ม เพื่อป้องกันสนามแม่เหล็กภายนอก
3.6 เครื่องวัดแบบเทอร์โมคัปเปิล (Thermocouple Meter)
เครื่องวัดนี้มีชื่อหลักการทำงานของเทอร์โมคัปเปิล ประกอบด้วยโลหะ 2 ชนิดที่ต่างกัน ซึ่งจะเกิดความต่างศํกย์ (Potential Difference; EMS) ประมาณ 0 - 10mV
ขึ้นที่รอยต่อระหว่างโลหะทั้งสอง ความต่างศักย์นี้เกิดจากอุณหภูมิที่แตกต่างที่รอยต่อ จึงเป็นเหตุทำให้เกิดกระแสไหลผ่านมิเตอร์มูฟเม้นท์
รูปที่ 3.7 แสดงสเกลมิเตอร์แบบกฎกำลังสอง
3.5 ลักษณะจำเพาะของเครื่องวัดแบบอิเล็กโทรไดนาโม
1. สเกลของแอมมิเตอร์และโวลท์มิเตอร์จะมีลักษณะกฎกำลังสอง โดยประมาณ ส่วนสเกลของวัตต์มิเตอร์จะมีลักษณะเป็นเชิงเส้น
2. ต้นทุนในการผลิตสูงกว่า และมีการสูญเสียกำลังสูงกว่าเครื่องวัดแบบ PMMC
3. ใช้วัดค่า rms ของรูปคลื่นกระแสสลับ โดยไม่คำนึงถึงรูปร่างของคลื่น
4. เหมาะสำหรับใช้ทั้งวงจรกระแสตรงและกระแสสลับ โดยไม่ถูกกระทบกระเทือนโดยความถี่บางรุ่นสามารถใช้ในพิสัยความถี่จากกระแสตรงถึง 25 KHz
5. สนามแม่เหล็กรายรอบจะมีผลกระทบต่อการทำงานของเครื่องวัดแบบนี้ ดังนั้นจะต้องวางชุดขดลวดภายในส่วนที่ห่อหุ้ม เพื่อป้องกันสนามแม่เหล็กภายนอก
3.6 เครื่องวัดแบบเทอร์โมคัปเปิล (Thermocouple Meter)
เครื่องวัดนี้มีชื่อหลักการทำงานของเทอร์โมคัปเปิล ประกอบด้วยโลหะ 2 ชนิดที่ต่างกัน ซึ่งจะเกิดความต่างศํกย์ (Potential Difference; EMS) ประมาณ 0 - 10mV
ขึ้นที่รอยต่อระหว่างโลหะทั้งสอง ความต่างศักย์นี้เกิดจากอุณหภูมิที่แตกต่างที่รอยต่อ จึงเป็นเหตุทำให้เกิดกระแสไหลผ่านมิเตอร์มูฟเม้นท์
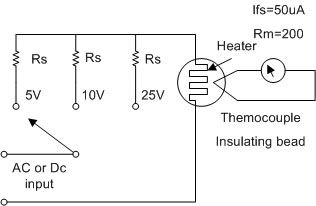
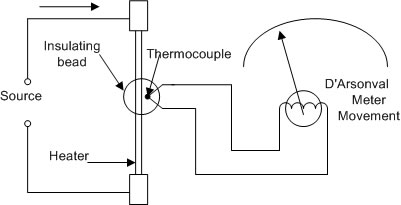 รูปที่ 3.8 แสดงวงจรเทอร์โมมิเตอร์คัปเปิล
เทอร์โมคัปเปิลนี้จะได้รับความร้อนจากขดลวดความร้อน (Heater Wire) ซึ่งจะเป็นตัวทำให้เกิดกระแสหรือโวลท์เตจที่จะทำการวัด เครื่องวัดชนิดนี้วัดได้อย่างกว้างขวาง
ซึ่งประมาณว่าวัดได้ตั้งแต่ 1 mA ถึง 50 A
รูปที่ 3.8 แสดงวงจรเทอร์โมมิเตอร์คัปเปิล
เทอร์โมคัปเปิลนี้จะได้รับความร้อนจากขดลวดความร้อน (Heater Wire) ซึ่งจะเป็นตัวทำให้เกิดกระแสหรือโวลท์เตจที่จะทำการวัด เครื่องวัดชนิดนี้วัดได้อย่างกว้างขวาง
ซึ่งประมาณว่าวัดได้ตั้งแต่ 1 mA ถึง 50 Aตัวอย่างที่ 11) จงหาค่า Rs ของโวลท์มิเตอร์แบบเทอร์โมคัปเปิล ที่มีย่านวัด 3 ย่านวัดคือ 5V, 10V และ 25V จากมิเตอร์มูฟเม้นท์ขนาด 50uA, Rm = 200W และมี รายละเอียดเกี่ยวกับลักษณะเฉพาะ ดังกราฟต่อไปนี้
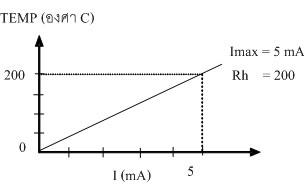 การเปลี่ยนแปลงระหว่างกระแสไฟฟ้า และอุณหภูมิที่ขดลวดความร้อน
การเปลี่ยนแปลงระหว่างกระแสไฟฟ้า และอุณหภูมิที่ขดลวดความร้อน
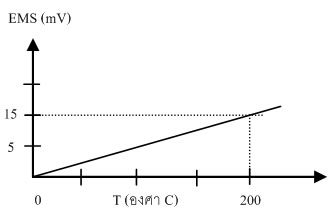 การเปลี่ยนแปลงระหว่างอุณหภูมิกับแรงดันไฟฟ้าที่จุดต่อของเทอร์โมคัปเปิล เขียนเป็นวงจรเทียบเคียงของโวลท์มิเตอร์แบบเทอร์โมคัปเปิลดังนี้
การเปลี่ยนแปลงระหว่างอุณหภูมิกับแรงดันไฟฟ้าที่จุดต่อของเทอร์โมคัปเปิล เขียนเป็นวงจรเทียบเคียงของโวลท์มิเตอร์แบบเทอร์โมคัปเปิลดังนี้
 จากรูป กราฟทำให้ทราบค่ากระแสสูงสุด Imax ที่จ่ายให้เครื่องวัด มีค่า 5mA
ย่านวัด 5V
จากรูป กราฟทำให้ทราบค่ากระแสสูงสุด Imax ที่จ่ายให้เครื่องวัด มีค่า 5mA
ย่านวัด 5V