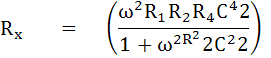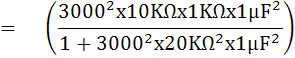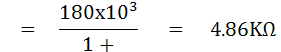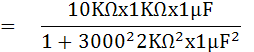บทที่ 5
เรื่อง เครื่องวัดแบบบริดจ์ (Bridge)
บริดจ์เป็นเครื่องมือที่ใช้วัดความต้านทาน (R), อินดักแตนซ์ (L) และคาปาซิแตนซ์ (C) ของวงจรไฟฟ้า ซึ่งอาศัยการเปรียบเทียบค่า R,L หรือ C ที่ทราบค่าแล้ว กับค่า R,L
หรือ C ที่ต้องการทราบค่าและใช้สภาพสมดุลของวงจรบริดจ์เป็นส่วนประกอบสำคัญของเครื่องวัดนี้ในการบอกค่าที่ต้องการทราบ
5.1 บริดจ์ไฟฟ้ากระแสตรง (DC Bridge)
DC Bridge เป็นเครื่องมือที่ใช้วัดความต้านทานในวงจรไฟฟ้ากระแสตรงซึ่งมีค่าความถูกต้องสูง ประเภทที่ใช้ในปัจจุบัน คือ วิทสโตนบริดจ์ (Wheatstone bridge)
5.1.1 วิทสโตนบริดจ์ (Wheatstone bridge)
วงจรภายในเครื่องวัดชนิดนี้ประกอบด้วย
1.) ตัวต้านทานที่ต่อขนานกัน 2 สาขา แต่ละสาขาประกอด้วยตัวต้านทาน 2 ตัวต่ออนุกรมกัน
2.) แหล่งจ่ายแรงดันไฟฟ้ากระแสตรง (E) ต่อขนานกับตัวต้านทานของวงจร ทำหน้าที่จ่ายกระแสไฟฟ้าให้กับวงจร
3.) กัลวานอมิเตอร์ (G) ซึ่งต่อกับขั้วสายที่ขนานกัน ทำหน้าที่ตรวจจับ (Detect) กระแสไฟฟ้าเพื่อบ่งบอกสภาพของวงจร ในกรณีที่บริดจ์สมดุลเข็มจะชี้ที่ศูนย์
แต่ถ้าไม่สมดุลเข็มจะเบี่ยงเบน ในการพิจารณา วิทสโตนบริดจ์แบ่งออกเป็น 2 สภาวะ คือ บริดจ์สมดุลและบริดจ์ไม่สมดุล
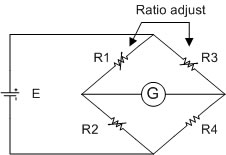 รูปที่ 5.1 แสดงวงจรวิทสโตนบริดจ์
1) บริดจ์สมดุล (Balanced Bridge)
รูปที่ 5.1 แสดงวงจรวิทสโตนบริดจ์
1) บริดจ์สมดุล (Balanced Bridge)
ขณะที่บริดจ์อยู่ในสภาวะสมดุลจะไม่มีกระแสไฟฟ้าไหลผ่านกัลวานอมิเตอร์ ทำให้เข็มของเครื่องวัดชี้ที่ 0
จากรูปที่ 5.1 ถ้าเราต้องการทราบค่า R4 จะต้องปรับอัตราส่วนของความต้านทาน R1/R2 (Ratio adjust) และปรับ R3 จนกระทั่งกระแสไหลผ่านกัลวานอมิเตอร์เป็น 0
แสดงว่าบริดจ์สมดุลจากสภาพนี้จะเห็นว่า แรงดันตกคร่อม R 2 และ R4 เท่ากัน และจะได้สมการดังนี้
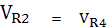
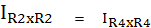
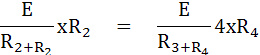
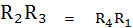 ดังนั้นเมื่อบริดจ์สมดุลจะได้สมการคือ
ดังนั้นเมื่อบริดจ์สมดุลจะได้สมการคือ
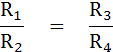
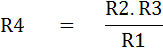 2) บริดจ์ไม่สมดุล (Unbalanced Bridge)
2) บริดจ์ไม่สมดุล (Unbalanced Bridge)
ขณะที่บริดจ์ไม่สมดุล จะมีกระแสไหลผ่านกัลวานอมิเตอร์ ทำให้เข็มของเครื่องวัดเบี่ยงเบนได้การเบี่ยงเบนของเข็มจะมากหรือน้อยขึ้นอยู่กับความไวของกัลวานอ
มิเตอร์ด้วย กล่าวคือ ถ้ามี กัลวานอมิเตอร์ 2 เครื่อง ในแต่ละเครื่องมีกระแสไหลผ่านเท่ากัน เข็มของกัลวานอมิเตอร์ที่มีความไวสูงกว่าก็จะเบี่ยงเบนได้มากกว่านั่นเอง
การหาความไวของกัลวานอมิเตอร์ทำได้อีกแบบคือหาในรูปของระยะการเบี่ยงเบนของเข็มต่อจำนวนกระแสที่ไหลผ่าน หรือ มุมการเบี่ยงเบนของเข็มต่อจำนวนกระ
แสไฟฟ้าที่ไหลผ่าน ดังสมการต่อไปนี้
S = มิลลิเมตร/uA หรือ องศา/uA หรือ เรเดียน/uA
ระยะการเบี่ยงเบนของเข็มหาได้จาก
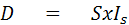 เมื่อ
D = ระยะการเบี่ยงเบนของเข็ม (ม.ม.)
เมื่อ
D = ระยะการเบี่ยงเบนของเข็ม (ม.ม.)
S = ความไวของกัลวานอมิเตอร์ (ม.ม. / uA)
Ig = กระแสที่ไหลผ่านกัลวานอมิเตอร์ (uA)
ปริมาณกระแสที่ไหลผ่านกัลวานอมิเตอร์ (Ig) ที่แสดงสภาพไม่สมดุลของวงจรหาได้โดยการนำทฤษฎี ทวินินมาร่วมวิเคราะห์ ดังนี้
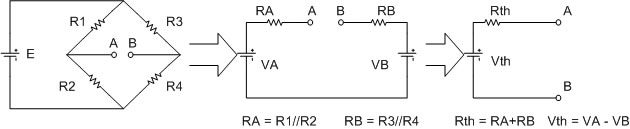 รูปที่ 5.2 แสดงการหา Ig โดยใช้ทฤษฎีทวินินมาร่วมวิเคราะห์
จากรูปที่ 5.2
รูปที่ 5.2 แสดงการหา Ig โดยใช้ทฤษฎีทวินินมาร่วมวิเคราะห์
จากรูปที่ 5.2
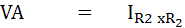
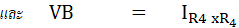
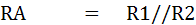
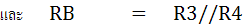 ดังนั้น Vetch ก็คือ ผลต่างของ VA และ VB ส่วน Rth ก็คือผลรวมของ RA กับ RB เมื่อได้ค่า Vetch และ Roth แล้วก็สามารถหาค่ากระแสที่ไหลผ่านกัลวานอมิเตอร์ได้ ดังนี้
ดังนั้น Vetch ก็คือ ผลต่างของ VA และ VB ส่วน Rth ก็คือผลรวมของ RA กับ RB เมื่อได้ค่า Vetch และ Roth แล้วก็สามารถหาค่ากระแสที่ไหลผ่านกัลวานอมิเตอร์ได้ ดังนี้
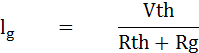 โดยที่ Rg คือ ความต้านทานภายในของกัลวานอมิเตอร์
ตัวอย่างที่ 1) จงหากระแสที่ไหลผ่านกัลวานอมิเตอร์ ที่มี Rg มีค่าเท่ากับ 200W ในขณะที่วงจร วิสโตนบริดจ์ อยู่ในสภาพไม่สมดุล
โดยที่ Rg คือ ความต้านทานภายในของกัลวานอมิเตอร์
ตัวอย่างที่ 1) จงหากระแสที่ไหลผ่านกัลวานอมิเตอร์ ที่มี Rg มีค่าเท่ากับ 200W ในขณะที่วงจร วิสโตนบริดจ์ อยู่ในสภาพไม่สมดุล
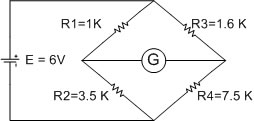 จากวงจร จะสามารถหาค่า Rth และ Vth โดยใช้ทฤษฎีทวินินได้ ดังนี้
จากวงจร จะสามารถหาค่า Rth และ Vth โดยใช้ทฤษฎีทวินินได้ ดังนี้
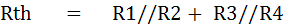
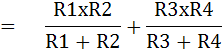
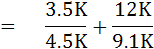
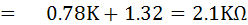
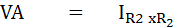
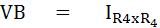
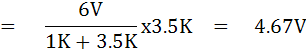
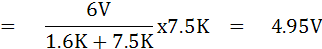
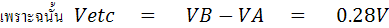
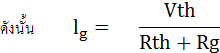
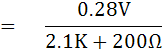
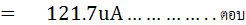 5.1.2 วิทสโตนบริดจ์ที่มีค่าความต้านทานต่างกันเล็กน้อย (Slightly Unbalanced Bridge)
ในการหาค่าความต้านทานด้วยวิทสโตนบริดจ์ นั้นค่าความต้านทานแต่ละตัวในวงจรมีค่าแตกต่างกัน ในกรณีที่ตัวต้านทาน 3 ใน 4 ตัวที่อยู่ในวงจรมีค่าเท่ากัน
(คือ R) ส่วนความต้านทานตัวที่ 4 มีค่าต่างไปจากค่าความต้านทาน 3 ตัวแรกเพียงเล็กน้อย คือ 1 - 5 % (r) ในการหาแรงดันและความต้านทานเทียบเคียงเทวินินนั้น มักใช้ค่าโดย
ประมาณซึ่งให้ผลลัพธ์ใกล้เคียงกับความจริง ช่วยให้สมการของวงจรเทียบเคียงเทวินินสั้นและง่ายต่อการหาค่าต่างๆ ในวงจร
5.1.2 วิทสโตนบริดจ์ที่มีค่าความต้านทานต่างกันเล็กน้อย (Slightly Unbalanced Bridge)
ในการหาค่าความต้านทานด้วยวิทสโตนบริดจ์ นั้นค่าความต้านทานแต่ละตัวในวงจรมีค่าแตกต่างกัน ในกรณีที่ตัวต้านทาน 3 ใน 4 ตัวที่อยู่ในวงจรมีค่าเท่ากัน
(คือ R) ส่วนความต้านทานตัวที่ 4 มีค่าต่างไปจากค่าความต้านทาน 3 ตัวแรกเพียงเล็กน้อย คือ 1 - 5 % (r) ในการหาแรงดันและความต้านทานเทียบเคียงเทวินินนั้น มักใช้ค่าโดย
ประมาณซึ่งให้ผลลัพธ์ใกล้เคียงกับความจริง ช่วยให้สมการของวงจรเทียบเคียงเทวินินสั้นและง่ายต่อการหาค่าต่างๆ ในวงจร
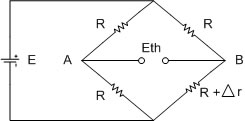 รูปที่ 5.3 แสดงวงจร Slightly Unbalanced Bridge
จากรูปที่ 5.3 เมื่อ บริดจ์ไม่สมดุล จะได้
รูปที่ 5.3 แสดงวงจร Slightly Unbalanced Bridge
จากรูปที่ 5.3 เมื่อ บริดจ์ไม่สมดุล จะได้

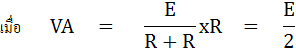
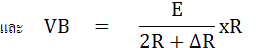
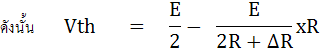
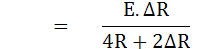
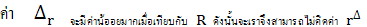 ก็จะได้
ก็จะได้
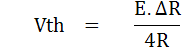
 ตัวอย่างที่ 2) จากรูปวงจร Slightly Unbalanced Bridge ค่าความต้านทานทั้งสามตัว = 500W ตัวที่ 4 มีค่ามากกว่าค่าความต้านทาน R = 5 % (525W) แรงดัน (E)
ที่จ่ายให้กับวงจร = 10V จงหาค่ากระแสที่ไหลผ่านกัลวานอมิเตอร์ที่มีความต้านทานภายใน 125W
ตัวอย่างที่ 2) จากรูปวงจร Slightly Unbalanced Bridge ค่าความต้านทานทั้งสามตัว = 500W ตัวที่ 4 มีค่ามากกว่าค่าความต้านทาน R = 5 % (525W) แรงดัน (E)
ที่จ่ายให้กับวงจร = 10V จงหาค่ากระแสที่ไหลผ่านกัลวานอมิเตอร์ที่มีความต้านทานภายใน 125W
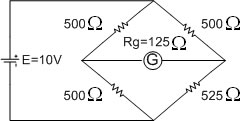 จากสมการ
จากสมการ
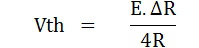
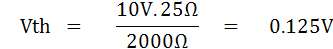

 ดังนั้นค่ากระแสที่ไหลผ่านกัลวานอมิเตอร์จะมีค่าเท่ากับ
ดังนั้นค่ากระแสที่ไหลผ่านกัลวานอมิเตอร์จะมีค่าเท่ากับ
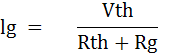
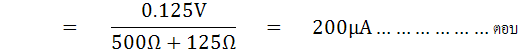 5.1.3 เคลวินบริดจ์ (Kelvin Bridge)
5.1.3 เคลวินบริดจ์ (Kelvin Bridge)
ใน Wheatstone Bridge สายและขั้วต่อจะมีความต้านทานอยู่จำนวนหนึ่งดังนั้นการนำ Wheatstone Bridge มาวัดความต้านทานที่มีค่าต่ำ (0.1uW – 100W)
จะทำให้ค่าที่อ่านได้จากเครื่องวัดมีความคลาดเคลื่อนไปเนื่องจากอัตราส่วนของความต้านทานที่ทำให้วงจรบริดจ์จะรวมค่าความต้านทานของสายและขั้วต่อเข้าไปด้วยวิธีการลดผลกระ
ทบจากความต้านทานของสายและขั้วต่อของ Wheatstone Bridge โดยการนำอัตราส่วนความต้านทานอีกค่าหนึ่ง RB/RA ต่อเพิ่มเข้าไปในวงจร (Rica) เราเรียกวงจรนี้ว่า เควินบริดจ์
(Kelvin Bridge) ขณะที่ Kelvin Bridge อยู่ในสภาวะสมดุลย์ แสดงว่าอัตรส่วนความต้านทานของวงจรคือ
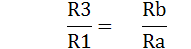 เมื่อนำกฎการแบ่งแรงดันมาพิจารณาจะได้สมการไฟฟ้าที่จุด A คือ
เมื่อนำกฎการแบ่งแรงดันมาพิจารณาจะได้สมการไฟฟ้าที่จุด A คือ
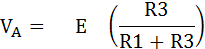 แรงดันไฟฟ้าที่จุด B ไปยังขั้วลบของแหล่งจ่ายเป็นผลรวมของแรงดันตกคร่อม Rx และ Rb เขียนสมการได้ดังนี้ในกรณีที่วงจรบริดจ์สมดุลแรงดันไฟฟ้า VA=VB
แรงดันไฟฟ้าที่จุด B ไปยังขั้วลบของแหล่งจ่ายเป็นผลรวมของแรงดันตกคร่อม Rx และ Rb เขียนสมการได้ดังนี้ในกรณีที่วงจรบริดจ์สมดุลแรงดันไฟฟ้า VA=VB
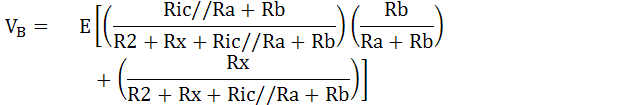
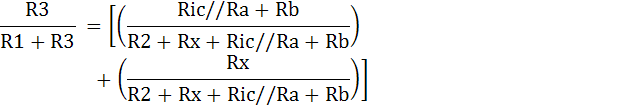 แก้สมการจะได้ค่า Rx ดังนี้
แก้สมการจะได้ค่า Rx ดังนี้
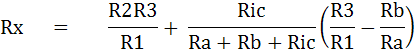
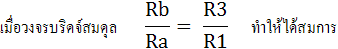
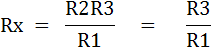
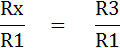 ดังนั้นเมื่อ Kelvin Bridge r1สมดุล อาจกล่าวได้ว่า
ดังนั้นเมื่อ Kelvin Bridge r1สมดุล อาจกล่าวได้ว่า
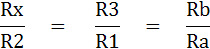 ตัวอย่าง จงหาค่า Rx ในรูป เมื่ออัตราส่วนความต้านทาน จากสมการ
ตัวอย่าง จงหาค่า Rx ในรูป เมื่ออัตราส่วนความต้านทาน จากสมการ
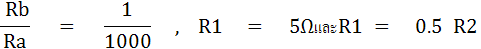
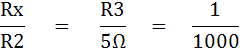 เมื่อ R1 = 0.5 R2 จึงหาค่า R2 ได้ดังนี้
เมื่อ R1 = 0.5 R2 จึงหาค่า R2 ได้ดังนี้
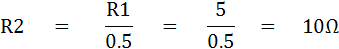
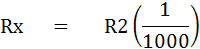
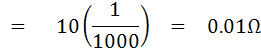 5.1.4 การนำบริดจ์ฟ้ากระแสตรงไปใช้งาน
บริดจ์นำมาใช้ในการวัดและควบคุมการผลิตชิ้นงานทางด้านอุตสาหกรรมได้มากมาย เช่น นำ Wheatstone bridge มาใช้วัดความต้านทานในลวดประเภทต่างๆ
ไม่ว่าจะเป็นการควบคุมคุณภาพของตัวเส้นลวด หรืออุปกรณ์ที่ประกอบด้วยเส้นลวด ได้แก่ การวัดความต้านทานของขดลวดพันมอเตอร์, หม้อแปลงไฟฟ้า, ขดลวด Solenoids และขด
ลวดในรีเลย์เป็นต้น
5.1.4 การนำบริดจ์ฟ้ากระแสตรงไปใช้งาน
บริดจ์นำมาใช้ในการวัดและควบคุมการผลิตชิ้นงานทางด้านอุตสาหกรรมได้มากมาย เช่น นำ Wheatstone bridge มาใช้วัดความต้านทานในลวดประเภทต่างๆ
ไม่ว่าจะเป็นการควบคุมคุณภาพของตัวเส้นลวด หรืออุปกรณ์ที่ประกอบด้วยเส้นลวด ได้แก่ การวัดความต้านทานของขดลวดพันมอเตอร์, หม้อแปลงไฟฟ้า, ขดลวด Solenoids และขด
ลวดในรีเลย์เป็นต้น
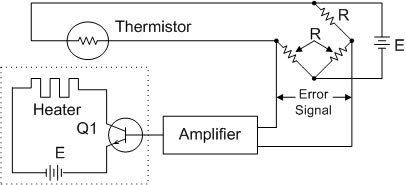 รูปที่ 5.4 แสดงวงจรบริดจ์ที่ใช้ในการควบคุมความร้อนเบื้องต้น
จากรูปเป็นวงจรบริดจ์ที่ใช้ในการควบคุมความร้อนแบบพื้นฐาน (Basic Bridge Controller Heater Circuit) มีหลักการทำงานคือ ขณะอุณหภูมิอยู่ในสภาพความต้องการ
Thermistor จะมีความต้านทานเท่ากับ R วงจรบริดจ์จะอยู่ในสภาพสมดุล ดังนั้นจึงไม่มี Error Signal ซึ่งอยู่ในรูปของ Error Voltage เข้าไปไบอัสทรานซีสเตอร์จึงไม่มีกระแสไหลผ่าน
Heater ถ้าอุณหภูมิลดลง Thermistor จะมีความต้านทานลดลงไม่เท่ากับ R ดังนั้นวงจรบริดจ์จึงไม่สมดุล ทำให้เกิด Error Voltage แล้วได้รับการขยายให้มีขนาดพอที่จะไบอัสทราน
ซีสเตอร์ ทำให้มีกระแสไหลผ่าน Heater ส่งผลให้อุณหภูมิและความต้านทานของ Thermistor มีค่ามากขึ้น จนกระทั่งความต้านทานมีค่าเท่ากับ R วงจรจะอยู่ในสภาวะสมดุลอีกครั้ง
5.2 บริดจ์ไฟฟ้ากระแสสลับ (AC Bridge)
รูปที่ 5.4 แสดงวงจรบริดจ์ที่ใช้ในการควบคุมความร้อนเบื้องต้น
จากรูปเป็นวงจรบริดจ์ที่ใช้ในการควบคุมความร้อนแบบพื้นฐาน (Basic Bridge Controller Heater Circuit) มีหลักการทำงานคือ ขณะอุณหภูมิอยู่ในสภาพความต้องการ
Thermistor จะมีความต้านทานเท่ากับ R วงจรบริดจ์จะอยู่ในสภาพสมดุล ดังนั้นจึงไม่มี Error Signal ซึ่งอยู่ในรูปของ Error Voltage เข้าไปไบอัสทรานซีสเตอร์จึงไม่มีกระแสไหลผ่าน
Heater ถ้าอุณหภูมิลดลง Thermistor จะมีความต้านทานลดลงไม่เท่ากับ R ดังนั้นวงจรบริดจ์จึงไม่สมดุล ทำให้เกิด Error Voltage แล้วได้รับการขยายให้มีขนาดพอที่จะไบอัสทราน
ซีสเตอร์ ทำให้มีกระแสไหลผ่าน Heater ส่งผลให้อุณหภูมิและความต้านทานของ Thermistor มีค่ามากขึ้น จนกระทั่งความต้านทานมีค่าเท่ากับ R วงจรจะอยู่ในสภาวะสมดุลอีกครั้ง
5.2 บริดจ์ไฟฟ้ากระแสสลับ (AC Bridge)
AC Bridge เป็นเครื่องวัดที่ใช้หลักการพื้นฐานของวิทสโตนบริดจ์ เพื่อหาค่าความต้านทาน (Resistance), อินดักแตนซ์ (Inductance) และคาปาซิแตนซ์ (Capacitance)
แขนของวงจรบริดจ์จะประกอบไปด้วยอิมพีแดนซ์ (Z) 4 ตัว แหล่งจ่ายแรงดันกระแสสลับ และเครื่องตรวจจับความเปลี่ยนแปลงไฟฟ้ากระแสสลับ (ac Detector) ดังรูปที่ 4.4
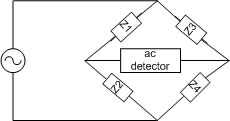 รูปที่ 5.5 แสดงวงจร Ac Bridge
จากรูปที่ 5.5 ขณะที่เครื่องวัดความเปลี่ยนแปลงของกระแสอ่านค่าเท่ากับศูนย์ ทำให้ทราบว่าวงจรบริดจ์นี้สมดุล และเมื่อบริดจ์สมดุลจะได้สมการดังนี้
รูปที่ 5.5 แสดงวงจร Ac Bridge
จากรูปที่ 5.5 ขณะที่เครื่องวัดความเปลี่ยนแปลงของกระแสอ่านค่าเท่ากับศูนย์ ทำให้ทราบว่าวงจรบริดจ์นี้สมดุล และเมื่อบริดจ์สมดุลจะได้สมการดังนี้
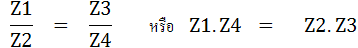 โดยที่ Z หมายถึง อิมแดนซ์ ที่อยู่ในรูปของ Complex Number (Real Part + Imaginary Part) ที่ประกอบด้วย Resisitance (R) กับ Capacitance (XC) หรือ
Resisitance (R) กับ Inductance (XL) หรืออาจมีแต่ Resistance, Capacitance, Inductance อย่างใดอย่างหนึ่งเพียงอย่างเดียวก็ได้ค่าของ Z แบ่งได้เป็น 2 ลักษณะคือ
1) ค่า Z ที่อยู่ในรูปของวงจรอนุกรม (Series) ที่ประกอบด้วย Resistance อนุกรมกับค่า Capacitance (Xc) หรือ Inductance (XL) เขียนเป็นสมกาได้ดังนี้
โดยที่ Z หมายถึง อิมแดนซ์ ที่อยู่ในรูปของ Complex Number (Real Part + Imaginary Part) ที่ประกอบด้วย Resisitance (R) กับ Capacitance (XC) หรือ
Resisitance (R) กับ Inductance (XL) หรืออาจมีแต่ Resistance, Capacitance, Inductance อย่างใดอย่างหนึ่งเพียงอย่างเดียวก็ได้ค่าของ Z แบ่งได้เป็น 2 ลักษณะคือ
1) ค่า Z ที่อยู่ในรูปของวงจรอนุกรม (Series) ที่ประกอบด้วย Resistance อนุกรมกับค่า Capacitance (Xc) หรือ Inductance (XL) เขียนเป็นสมกาได้ดังนี้
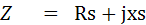
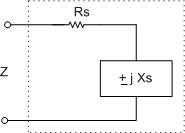 .
รูปที่ 5.6 แสดงค่า Z ที่อยู่ในรูปของวงจรอนุกรม
จากรูปที่ 5.6 ค่า Q ของวงจรหาได้จากสมการ
.
รูปที่ 5.6 แสดงค่า Z ที่อยู่ในรูปของวงจรอนุกรม
จากรูปที่ 5.6 ค่า Q ของวงจรหาได้จากสมการ
Qs = Xs / Rs
เมื่อ Xs = ค่าความต้านทานของ L หรือ C ในวงจรอนุกรม
Rs = ค่าความต้านทานของ R ในวงจรอนุกรม
2) ค่า Z ที่อยู่ในรูปของวงจรขนาน (Parallel) ที่ประกอบด้วย Resistance ขนานกับค่า Capacitance (XC) หรือ Inductance (XL) เขียนเป็นสมการได้ดังนี้
Z = Rp + jXp
 รูปที่ 5.7 แสดงค่า Z ที่อยู่ในรูปของวงจรขนาน
จากรูปที่ 5.7 ค่า Q ของวงจรหาได้จากสมการ
รูปที่ 5.7 แสดงค่า Z ที่อยู่ในรูปของวงจรขนาน
จากรูปที่ 5.7 ค่า Q ของวงจรหาได้จากสมการ
QP = Rp / Xp
เมื่อ Xp = ค่าความต้านทานของ L หรือ C ในวงจรขนาน
Rp = ค่าความต้านทานของ R ในวงจรขนาน
ในการที่เราจะทราบว่าบริดจ์จะสมดุลหรือไม่ จะต้องเทียบอัตราส่วนของอิมพีแดนซ์ทั้ง 4 ตัวซึ่งอิมพีแดนซ์แต่ละตัวจะต้องอยู่ในรูปของวงจรที่เหมือนกันจึงจะนำมาเปรียบ
เทียบได้ดังนั้นจึงจำเป็นต้องเปลี่ยนรูปอิมพีแดนซ์ของวงจรให้เหมือนกันเสียก่อน
5.2.1 การเปลี่ยนค่าอิมพีแดนซ์จากวงจรอนุกรมเป็นวงจรขนาน
จากสมการ วงจรอนุกรมจะได้
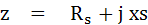
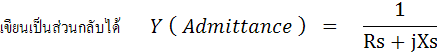
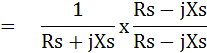
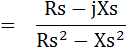
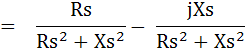 ดังนั้นเมื่อแยกค่า Real กับ Imaginary Part ออกจากกันจะได้ค่า Z ดังนี้
ดังนั้นเมื่อแยกค่า Real กับ Imaginary Part ออกจากกันจะได้ค่า Z ดังนี้
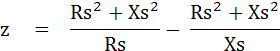 เราสามารถเขียนเป็นสมการในการเปลี่ยนรูปวงจรได้ดังนี้
เราสามารถเขียนเป็นสมการในการเปลี่ยนรูปวงจรได้ดังนี้
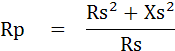
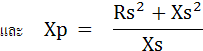 หรือหาได้ในรูปของ Q คือ
หรือหาได้ในรูปของ Q คือ
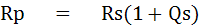
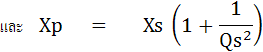 5.2.2 การเปลี่ยนค่าอิมพีแดนซ์จากวงจรขนานเป็นวงจรอนุกรม
5.2.2 การเปลี่ยนค่าอิมพีแดนซ์จากวงจรขนานเป็นวงจรอนุกรม
ในการเปลี่ยนรูปค่าอิมพีแดนซ์ (Z) ในรูปวงจรขนานให้เป็นวงจรอนุกรม จะใช้ค่า Q ของ วงจรขนาน มาใช้ ดังสมการต่อไปนี้
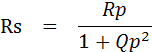
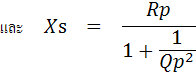 5.3 บริดจ์มุมเหมือน (Similar Angle Bridge)
Similar Angle Bridge เป็นวงจรบริดจ์กระแสสลับที่ใช้วัด Capacitive Impedance (Rx และCx) โดยใช้คาปาซิเตอร์มาตรฐาน (C2) เป็นองค์ประกอบในการเทียบค่า
5.3 บริดจ์มุมเหมือน (Similar Angle Bridge)
Similar Angle Bridge เป็นวงจรบริดจ์กระแสสลับที่ใช้วัด Capacitive Impedance (Rx และCx) โดยใช้คาปาซิเตอร์มาตรฐาน (C2) เป็นองค์ประกอบในการเทียบค่า
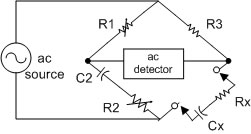 รูปที่ 5.8 แสดงวงจรบริดจ์มุมเหมือน
เมื่อบริดจ์สมดุล แล้วนำค่าต่างๆ ในวงจรไปเปรียบเทียบกันจะได้สมการ
รูปที่ 5.8 แสดงวงจรบริดจ์มุมเหมือน
เมื่อบริดจ์สมดุล แล้วนำค่าต่างๆ ในวงจรไปเปรียบเทียบกันจะได้สมการ
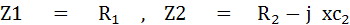
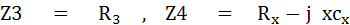 แทนค่าในสมการ
แทนค่าในสมการ
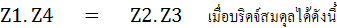
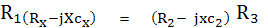 แยกสมการเป็น 2 ส่วนคือ สมการของจำนวนจริง กับสมการของจำนวนจินตภาพ จะได้
แยกสมการเป็น 2 ส่วนคือ สมการของจำนวนจริง กับสมการของจำนวนจินตภาพ จะได้

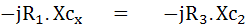 จากสมการจินตภาพจะได้
จากสมการจินตภาพจะได้
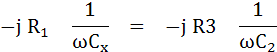
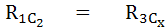 และจากสมการจำนวนจริงจะได้
และจากสมการจำนวนจริงจะได้
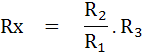
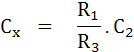 ตัวอย่าง Similar Angle Bridge ที่ใช้วัดค่า Capacitive Impedance ที่ความถี่ 2KHz และมีค่าคงที่ซึ่งทำให้บริดจ์อยู่ในสภาพสมดุลดังนี้
ตัวอย่าง Similar Angle Bridge ที่ใช้วัดค่า Capacitive Impedance ที่ความถี่ 2KHz และมีค่าคงที่ซึ่งทำให้บริดจ์อยู่ในสภาพสมดุลดังนี้

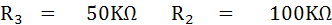 จงหาค่า RX และ CX ที่ต่อในวงจร
หาค่า RX จากสมการ
จงหาค่า RX และ CX ที่ต่อในวงจร
หาค่า RX จากสมการ

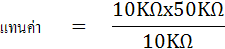
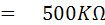 หาค่า CX จากสมการ
หาค่า CX จากสมการ
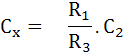 แทนค่า
แทนค่า
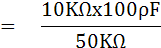
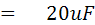 นำค่า RX และ CX มาเขียนเป็นวงจรเทียบเคียงได้เป็น
นำค่า RX และ CX มาเขียนเป็นวงจรเทียบเคียงได้เป็น
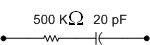 5.4 แมกซ์เวลส์บริดจ์ (Maxvell Bridge)
5.4 แมกซ์เวลส์บริดจ์ (Maxvell Bridge)
แมกซ์เวลส์บริดจ์ เป็นวงจรบริดจ์กระแสสลับที่ใช้วัด Inductive Impedance (RX และ LX) โดยใช้คาปาซิเตอร์มาตรฐาน (C1) เป็นองค์ประกอบที่สำคัญในการ
เปรียบเทียบค่า
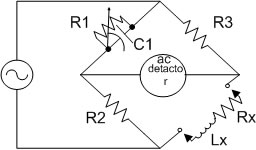 รูปที่ 5.9 แสดงแมกซ์เวลซ์บริดจ์
รูปที่ 5.9 แสดงแมกซ์เวลซ์บริดจ์
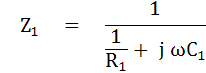
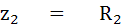

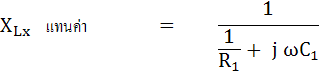
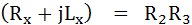
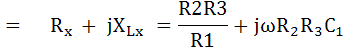 แยกเป็น 2 ส่วน
แยกเป็น 2 ส่วน
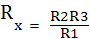
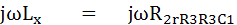
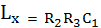 ตัวอย่าง Maxwell Bridge ใช้วัด Inductive Impedance ที่ความถี่ 2KHz และมีค่าคงที่ซึ่งทำให้บริดจ์สมดุลย์ คือ
ตัวอย่าง Maxwell Bridge ใช้วัด Inductive Impedance ที่ความถี่ 2KHz และมีค่าคงที่ซึ่งทำให้บริดจ์สมดุลย์ คือ
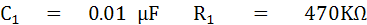
 จงหาค่า Rx และ Lx (1.09 KW , 5.1 H)
หาค่า RX และ LX ได้จากสมการ
จงหาค่า Rx และ Lx (1.09 KW , 5.1 H)
หาค่า RX และ LX ได้จากสมการ
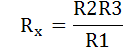
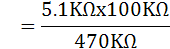
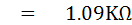 และ
และ

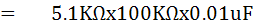
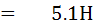 5.5 บริดจ์มุมตรงข้าม (Opposite Angle Bridge)
5.5 บริดจ์มุมตรงข้าม (Opposite Angle Bridge)
เป็นบริดจ์ที่ใช้วัดค่า Inductive Impedance ปกติจะใช้วงจรบริดจ์มุมเหมือน หาค่า Capacitive Impedance (CX และ RX) แต่ถ้าต้องการหาค่า Inductive
Impedance (LX และ RX) ทำได้โดยแทนค่าคาปาซิเตอร์มาตรฐาน (C2) เป็นอินดักเตอร์มาตรฐาน แต่เนื่องจากอินดักเตอร์มาตรฐาน มีขนาดใหญ่และราคาแพง ดังนั้นจึงใช้
คาปาซิเตอร์มาตรฐานแทน และจัดรูปวงจรใหม่ ดังรูปที่ 5.10
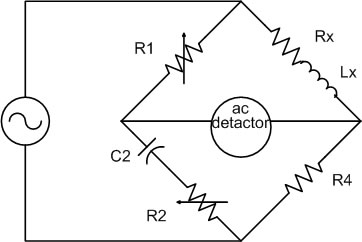 รูปที่ 5.10 แสดงวงจรบริดจ์มุมตรงข้าม หรือ เฮย์บริดจ์ (Hay Bridge)
เมื่อ Opposite Angle Bridge อยู่ในสภาพสมดุล แล้วนำค่าต่าง ๆในวงจรมาเปรียบเทียบจะได้
รูปที่ 5.10 แสดงวงจรบริดจ์มุมตรงข้าม หรือ เฮย์บริดจ์ (Hay Bridge)
เมื่อ Opposite Angle Bridge อยู่ในสภาพสมดุล แล้วนำค่าต่าง ๆในวงจรมาเปรียบเทียบจะได้
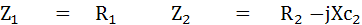
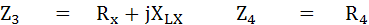 เมื่อ Bridge Balance
เมื่อ Bridge Balance
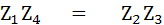
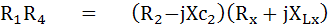
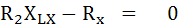
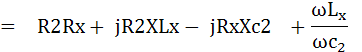 แยกเป็น 2 จำนวน
แยกเป็น 2 จำนวน
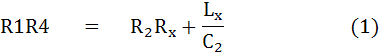 และ
และ
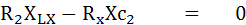
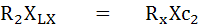
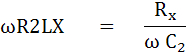
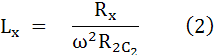 แทนค่า LX ใน (1)
แทนค่า LX ใน (1)
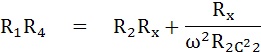
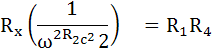

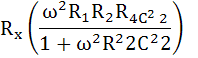
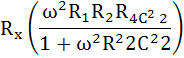 แทนค่าใน Rx ใน สมการที่ (2)
แทนค่าใน Rx ใน สมการที่ (2)
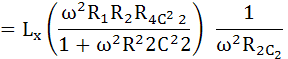 ตัวอย่าง บริดจ์มุมตรงข้าม มีค่าคงที่ที่ทำให้ Bridge Balance ดังนี้
w = 3000 red/S R1 = 10 KW
ตัวอย่าง บริดจ์มุมตรงข้าม มีค่าคงที่ที่ทำให้ Bridge Balance ดังนี้
w = 3000 red/S R1 = 10 KW
C2 = 1uF R4 = 1 KW
R2 = 2 KW
จงหาค่า RX และ LX
หาค่า RX และ CX ได้จากสมการ
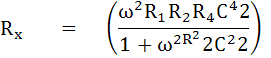
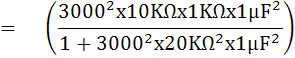
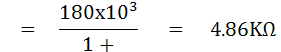
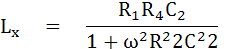
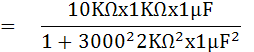
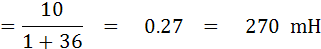
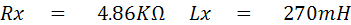
 รูปที่ 5.1 แสดงวงจรวิทสโตนบริดจ์
1) บริดจ์สมดุล (Balanced Bridge)
รูปที่ 5.1 แสดงวงจรวิทสโตนบริดจ์
1) บริดจ์สมดุล (Balanced Bridge)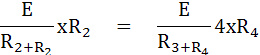
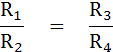
 รูปที่ 5.2 แสดงการหา Ig โดยใช้ทฤษฎีทวินินมาร่วมวิเคราะห์
จากรูปที่ 5.2
รูปที่ 5.2 แสดงการหา Ig โดยใช้ทฤษฎีทวินินมาร่วมวิเคราะห์
จากรูปที่ 5.2
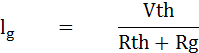 โดยที่ Rg คือ ความต้านทานภายในของกัลวานอมิเตอร์
ตัวอย่างที่ 1) จงหากระแสที่ไหลผ่านกัลวานอมิเตอร์ ที่มี Rg มีค่าเท่ากับ 200W ในขณะที่วงจร วิสโตนบริดจ์ อยู่ในสภาพไม่สมดุล
โดยที่ Rg คือ ความต้านทานภายในของกัลวานอมิเตอร์
ตัวอย่างที่ 1) จงหากระแสที่ไหลผ่านกัลวานอมิเตอร์ ที่มี Rg มีค่าเท่ากับ 200W ในขณะที่วงจร วิสโตนบริดจ์ อยู่ในสภาพไม่สมดุล
 จากวงจร จะสามารถหาค่า Rth และ Vth โดยใช้ทฤษฎีทวินินได้ ดังนี้
จากวงจร จะสามารถหาค่า Rth และ Vth โดยใช้ทฤษฎีทวินินได้ ดังนี้
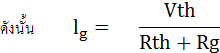
 รูปที่ 5.3 แสดงวงจร Slightly Unbalanced Bridge
จากรูปที่ 5.3 เมื่อ บริดจ์ไม่สมดุล จะได้
รูปที่ 5.3 แสดงวงจร Slightly Unbalanced Bridge
จากรูปที่ 5.3 เมื่อ บริดจ์ไม่สมดุล จะได้ จากสมการ
จากสมการ
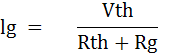
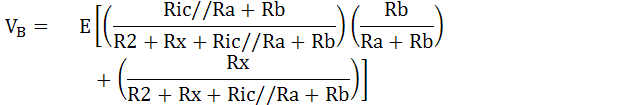
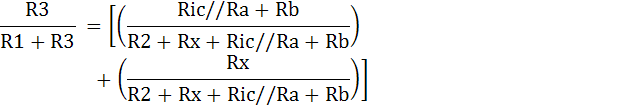 แก้สมการจะได้ค่า Rx ดังนี้
แก้สมการจะได้ค่า Rx ดังนี้
 รูปที่ 5.4 แสดงวงจรบริดจ์ที่ใช้ในการควบคุมความร้อนเบื้องต้น
จากรูปเป็นวงจรบริดจ์ที่ใช้ในการควบคุมความร้อนแบบพื้นฐาน (Basic Bridge Controller Heater Circuit) มีหลักการทำงานคือ ขณะอุณหภูมิอยู่ในสภาพความต้องการ
Thermistor จะมีความต้านทานเท่ากับ R วงจรบริดจ์จะอยู่ในสภาพสมดุล ดังนั้นจึงไม่มี Error Signal ซึ่งอยู่ในรูปของ Error Voltage เข้าไปไบอัสทรานซีสเตอร์จึงไม่มีกระแสไหลผ่าน
Heater ถ้าอุณหภูมิลดลง Thermistor จะมีความต้านทานลดลงไม่เท่ากับ R ดังนั้นวงจรบริดจ์จึงไม่สมดุล ทำให้เกิด Error Voltage แล้วได้รับการขยายให้มีขนาดพอที่จะไบอัสทราน
ซีสเตอร์ ทำให้มีกระแสไหลผ่าน Heater ส่งผลให้อุณหภูมิและความต้านทานของ Thermistor มีค่ามากขึ้น จนกระทั่งความต้านทานมีค่าเท่ากับ R วงจรจะอยู่ในสภาวะสมดุลอีกครั้ง
5.2 บริดจ์ไฟฟ้ากระแสสลับ (AC Bridge)
รูปที่ 5.4 แสดงวงจรบริดจ์ที่ใช้ในการควบคุมความร้อนเบื้องต้น
จากรูปเป็นวงจรบริดจ์ที่ใช้ในการควบคุมความร้อนแบบพื้นฐาน (Basic Bridge Controller Heater Circuit) มีหลักการทำงานคือ ขณะอุณหภูมิอยู่ในสภาพความต้องการ
Thermistor จะมีความต้านทานเท่ากับ R วงจรบริดจ์จะอยู่ในสภาพสมดุล ดังนั้นจึงไม่มี Error Signal ซึ่งอยู่ในรูปของ Error Voltage เข้าไปไบอัสทรานซีสเตอร์จึงไม่มีกระแสไหลผ่าน
Heater ถ้าอุณหภูมิลดลง Thermistor จะมีความต้านทานลดลงไม่เท่ากับ R ดังนั้นวงจรบริดจ์จึงไม่สมดุล ทำให้เกิด Error Voltage แล้วได้รับการขยายให้มีขนาดพอที่จะไบอัสทราน
ซีสเตอร์ ทำให้มีกระแสไหลผ่าน Heater ส่งผลให้อุณหภูมิและความต้านทานของ Thermistor มีค่ามากขึ้น จนกระทั่งความต้านทานมีค่าเท่ากับ R วงจรจะอยู่ในสภาวะสมดุลอีกครั้ง
5.2 บริดจ์ไฟฟ้ากระแสสลับ (AC Bridge) รูปที่ 5.5 แสดงวงจร Ac Bridge
จากรูปที่ 5.5 ขณะที่เครื่องวัดความเปลี่ยนแปลงของกระแสอ่านค่าเท่ากับศูนย์ ทำให้ทราบว่าวงจรบริดจ์นี้สมดุล และเมื่อบริดจ์สมดุลจะได้สมการดังนี้
รูปที่ 5.5 แสดงวงจร Ac Bridge
จากรูปที่ 5.5 ขณะที่เครื่องวัดความเปลี่ยนแปลงของกระแสอ่านค่าเท่ากับศูนย์ ทำให้ทราบว่าวงจรบริดจ์นี้สมดุล และเมื่อบริดจ์สมดุลจะได้สมการดังนี้
 .
รูปที่ 5.6 แสดงค่า Z ที่อยู่ในรูปของวงจรอนุกรม
จากรูปที่ 5.6 ค่า Q ของวงจรหาได้จากสมการ
.
รูปที่ 5.6 แสดงค่า Z ที่อยู่ในรูปของวงจรอนุกรม
จากรูปที่ 5.6 ค่า Q ของวงจรหาได้จากสมการ รูปที่ 5.7 แสดงค่า Z ที่อยู่ในรูปของวงจรขนาน
จากรูปที่ 5.7 ค่า Q ของวงจรหาได้จากสมการ
รูปที่ 5.7 แสดงค่า Z ที่อยู่ในรูปของวงจรขนาน
จากรูปที่ 5.7 ค่า Q ของวงจรหาได้จากสมการ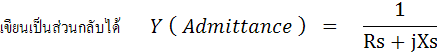
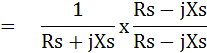
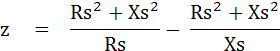 เราสามารถเขียนเป็นสมการในการเปลี่ยนรูปวงจรได้ดังนี้
เราสามารถเขียนเป็นสมการในการเปลี่ยนรูปวงจรได้ดังนี้
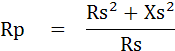
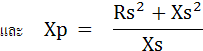 หรือหาได้ในรูปของ Q คือ
หรือหาได้ในรูปของ Q คือ
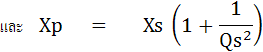 5.2.2 การเปลี่ยนค่าอิมพีแดนซ์จากวงจรขนานเป็นวงจรอนุกรม
5.2.2 การเปลี่ยนค่าอิมพีแดนซ์จากวงจรขนานเป็นวงจรอนุกรม 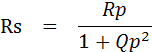
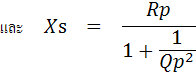 5.3 บริดจ์มุมเหมือน (Similar Angle Bridge)
Similar Angle Bridge เป็นวงจรบริดจ์กระแสสลับที่ใช้วัด Capacitive Impedance (Rx และCx) โดยใช้คาปาซิเตอร์มาตรฐาน (C2) เป็นองค์ประกอบในการเทียบค่า
5.3 บริดจ์มุมเหมือน (Similar Angle Bridge)
Similar Angle Bridge เป็นวงจรบริดจ์กระแสสลับที่ใช้วัด Capacitive Impedance (Rx และCx) โดยใช้คาปาซิเตอร์มาตรฐาน (C2) เป็นองค์ประกอบในการเทียบค่า
 รูปที่ 5.8 แสดงวงจรบริดจ์มุมเหมือน
เมื่อบริดจ์สมดุล แล้วนำค่าต่างๆ ในวงจรไปเปรียบเทียบกันจะได้สมการ
รูปที่ 5.8 แสดงวงจรบริดจ์มุมเหมือน
เมื่อบริดจ์สมดุล แล้วนำค่าต่างๆ ในวงจรไปเปรียบเทียบกันจะได้สมการ
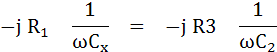
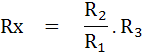
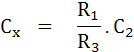 ตัวอย่าง Similar Angle Bridge ที่ใช้วัดค่า Capacitive Impedance ที่ความถี่ 2KHz และมีค่าคงที่ซึ่งทำให้บริดจ์อยู่ในสภาพสมดุลดังนี้
ตัวอย่าง Similar Angle Bridge ที่ใช้วัดค่า Capacitive Impedance ที่ความถี่ 2KHz และมีค่าคงที่ซึ่งทำให้บริดจ์อยู่ในสภาพสมดุลดังนี้

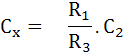 แทนค่า
แทนค่า
 รูปที่ 5.9 แสดงแมกซ์เวลซ์บริดจ์
รูปที่ 5.9 แสดงแมกซ์เวลซ์บริดจ์
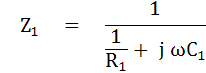
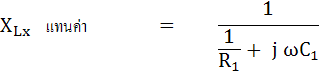
 รูปที่ 5.10 แสดงวงจรบริดจ์มุมตรงข้าม หรือ เฮย์บริดจ์ (Hay Bridge)
เมื่อ Opposite Angle Bridge อยู่ในสภาพสมดุล แล้วนำค่าต่าง ๆในวงจรมาเปรียบเทียบจะได้
รูปที่ 5.10 แสดงวงจรบริดจ์มุมตรงข้าม หรือ เฮย์บริดจ์ (Hay Bridge)
เมื่อ Opposite Angle Bridge อยู่ในสภาพสมดุล แล้วนำค่าต่าง ๆในวงจรมาเปรียบเทียบจะได้
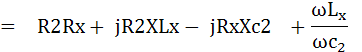 แยกเป็น 2 จำนวน
แยกเป็น 2 จำนวน
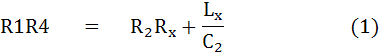 และ
และ
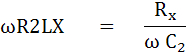
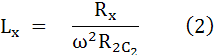 แทนค่า LX ใน (1)
แทนค่า LX ใน (1)
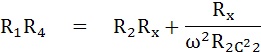
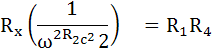

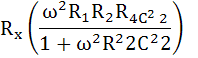
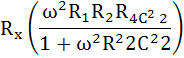 แทนค่าใน Rx ใน สมการที่ (2)
แทนค่าใน Rx ใน สมการที่ (2)
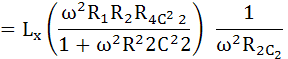 ตัวอย่าง บริดจ์มุมตรงข้าม มีค่าคงที่ที่ทำให้ Bridge Balance ดังนี้
w = 3000 red/S R1 = 10 KW
ตัวอย่าง บริดจ์มุมตรงข้าม มีค่าคงที่ที่ทำให้ Bridge Balance ดังนี้
w = 3000 red/S R1 = 10 KW