4. โอห์มมิเตอร์ (Ohmmeter)
4.1 โอห์มมิเตอร์แบบอนุกรม (Series Ohmmeter) เป็นโอห์มมิเตอร์อย่างง่าย ประกอบด้วยแบตตอรี่, แอมมิเตอร์ และความต้านทานปรับค่าได้ ดังรูปที่ 2.13
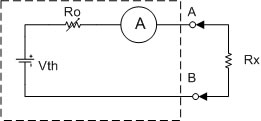 รูปที่ 2.13 แสดงวงจรโอห์มมิเตอร์อย่างง่าย
Ro คือ Thevenin Resistance ของโอห์มมิเตอร์ รวมทั้งความต้านทานในของแอมมิเตอร์ Vth คือ ค่า Open Circuit Voltage ของโอห์มมิเตอร์ที่ขั้ววัด
A – B โดยทั่วไป Ro จะเป็นตัวต้านทานชนิดปรับค่าได้ เพื่อคอยปรับให้เข็มของมิเตอร์ชี้ที่ค่าศูนย์โอห์มเสมอเมื่อลัดวงจร (Short) สาย A – B เข้าด้วยกัน ซึ่ง Ro จะปรับให้กระแส
ไหลผ่านแอมมิเตอร์เต็มสเกลพอดี ดังสมการต่อไปนี้
เมื่อ Short สาย A - B
รูปที่ 2.13 แสดงวงจรโอห์มมิเตอร์อย่างง่าย
Ro คือ Thevenin Resistance ของโอห์มมิเตอร์ รวมทั้งความต้านทานในของแอมมิเตอร์ Vth คือ ค่า Open Circuit Voltage ของโอห์มมิเตอร์ที่ขั้ววัด
A – B โดยทั่วไป Ro จะเป็นตัวต้านทานชนิดปรับค่าได้ เพื่อคอยปรับให้เข็มของมิเตอร์ชี้ที่ค่าศูนย์โอห์มเสมอเมื่อลัดวงจร (Short) สาย A – B เข้าด้วยกัน ซึ่ง Ro จะปรับให้กระแส
ไหลผ่านแอมมิเตอร์เต็มสเกลพอดี ดังสมการต่อไปนี้
เมื่อ Short สาย A - B
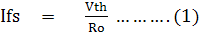 เมื่อนำค่าความต้านทานไม่ทราบค่า (Rx) มาวัดโดยต่อที่ขั้ว A – B ขณะนี้กระแสในวงจรคือ
เมื่อนำค่าความต้านทานไม่ทราบค่า (Rx) มาวัดโดยต่อที่ขั้ว A – B ขณะนี้กระแสในวงจรคือ
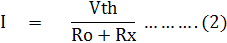 จากสมการที่ (1) และ (2) จะได้
จากสมการที่ (1) และ (2) จะได้
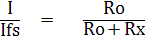
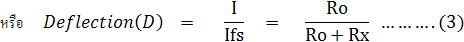 !!จากสมการ (3) สามารถนำมาใช้เป็นประโยชน์ในการเขียนสเกล ของโอห์มมิเตอร์ได้
!!จากสมการ (3) สามารถนำมาใช้เป็นประโยชน์ในการเขียนสเกล ของโอห์มมิเตอร์ได้
Rx |
D |
0
Ro/3
Ro
3 Ro
7 Ro
¥
|
1
3/4
1/2
1/4
1/8
0
|
ตารางที่ 2.1
จากตารางที่ 2.1 ค่า Rx และค่า D ได้จากการแทนค่า Rx ในสมการ (3) จะเห็นว่า เมื่อ Rx เท่ากับศูนย์โอห์ม (Short สาย A – B) จะได้ค่า D เท่ากับ 1 หรือ
Full Scale Deflection ดังนั้น ณ จุดที่เข็มมิเตอร์ชี้เต็มสเกลก็จะเทียบกับค่าความต้านทานศูนย์โอห์มบนสเกลของโอห์มมิเตอร์ และ Rx เท่ากับ Infinite หรือ Open Circuit
(สาย A – B ไม่ต่อกัน) จะได้ค่า D เท่ากับ 0 หรือ ไม่มีกระแสไหลในวงจรเข็มมิเตอร์จะอยู่กับที่ ดังนั้น ณ จุดนี้สามารถเขียนสเกลบนโอห์มมิเตอร์ได้เป็น Infinite Ohm และ
Rx เท่ากับจะได้ค่า D เท่ากับ 1/2 ดังนั้น ณ จุดนี้ก็สามารถเขียนสเกลบนโอห์มมิเตอร์ได้เท่ากับค่าความต้านทาน Ro
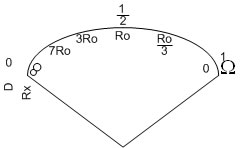 รูปที่ 2.14 แสดงสเกลของโอห์มมิเตอร์
จากสมการที่ (3) เราสามารถสร้างสเกลโดยการหาค่า Rx ในเทอมของ D และ Ro ได้
รูปที่ 2.14 แสดงสเกลของโอห์มมิเตอร์
จากสมการที่ (3) เราสามารถสร้างสเกลโดยการหาค่า Rx ในเทอมของ D และ Ro ได้
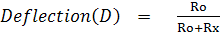
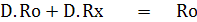
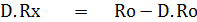
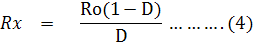 4.2 โอห์มมิเตอร์แบบ Shunt
ลักษณะของวงจรโอห์มมิเตอร์แบบ Shunt แสดงดังรูปที่ 2.15
4.2 โอห์มมิเตอร์แบบ Shunt
ลักษณะของวงจรโอห์มมิเตอร์แบบ Shunt แสดงดังรูปที่ 2.15
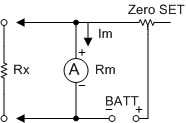 รูปที่ 2.15 แสดง Shunt Ohmmeter Circuit
หลักการทำงานของโอห์มมิเตอร์ชนิดนี้อาศัยการแบ่งกระแสในวงจรในขณะที่สายวัดทั้งสองแตะกัน หมายถึงความต้านทานเป็น ศูนย์ กระแสจากแบตเตอรี่จะไหลผ่าน
สายวัดทั้งสองเกือบทั้งหมด เข็มของมิเตอร์ก็จะไม่ขึ้นเพราะมีกระแสไหลผ่านน้อยมาก และกระแสในวงจรจะถูกจำกัดด้วยตัวต้านทาน Zero Set และในขณะที่สายวัดทั้งสองจากกัน
(ความต้านทาน Rx มีค่าสูง Infinite) กระแสจากแบตเตอรี่จะไหลผ่านแอมมิเตอร์ทั้งหมด เข็มของมิเตอร์ก็จะขึ้นเต็มสเกล ฉะนั้นโอห์มมิเตอร์แบบนี้จึงมีสเกลศูนย์โอห์มอยู่ทางซ้ายมือ
และค่าความต้านทานสูงถึง Infinite อยู่ทางขวามือเหมือนกับแอมมิเตอร์ทั่วไป ซึ่งจะกลับกับโอห์มมิเตอร์แบบอนุกรมในโอห์มมิเตอร์แบบอนุกรม ค่ากระแสที่ไหลในวงจรจะลดลงเมื่อ
ความต้านทานในวงจรเพิ่มมากขึ้น ซึ่งดูจากสมการ
รูปที่ 2.15 แสดง Shunt Ohmmeter Circuit
หลักการทำงานของโอห์มมิเตอร์ชนิดนี้อาศัยการแบ่งกระแสในวงจรในขณะที่สายวัดทั้งสองแตะกัน หมายถึงความต้านทานเป็น ศูนย์ กระแสจากแบตเตอรี่จะไหลผ่าน
สายวัดทั้งสองเกือบทั้งหมด เข็มของมิเตอร์ก็จะไม่ขึ้นเพราะมีกระแสไหลผ่านน้อยมาก และกระแสในวงจรจะถูกจำกัดด้วยตัวต้านทาน Zero Set และในขณะที่สายวัดทั้งสองจากกัน
(ความต้านทาน Rx มีค่าสูง Infinite) กระแสจากแบตเตอรี่จะไหลผ่านแอมมิเตอร์ทั้งหมด เข็มของมิเตอร์ก็จะขึ้นเต็มสเกล ฉะนั้นโอห์มมิเตอร์แบบนี้จึงมีสเกลศูนย์โอห์มอยู่ทางซ้ายมือ
และค่าความต้านทานสูงถึง Infinite อยู่ทางขวามือเหมือนกับแอมมิเตอร์ทั่วไป ซึ่งจะกลับกับโอห์มมิเตอร์แบบอนุกรมในโอห์มมิเตอร์แบบอนุกรม ค่ากระแสที่ไหลในวงจรจะลดลงเมื่อ
ความต้านทานในวงจรเพิ่มมากขึ้น ซึ่งดูจากสมการ
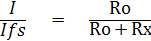 และเมื่อพิจารณาจากวงจรโอห์มมิเตอร์แบบ Shunt จะได้ว่า
และเมื่อพิจารณาจากวงจรโอห์มมิเตอร์แบบ Shunt จะได้ว่า
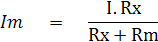
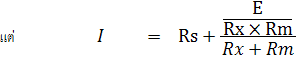
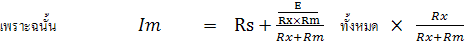
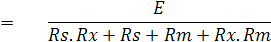
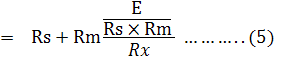 จากสมการ (5) จะเห็นว่า ถ้า Rx มีค่าเป็นศูนย์ จะให้กระแสที่ผ่านแอมมิเตอร์เป็นศูนย์ ถ้า Rx มีค่าสูง Infinite ก็จะมีกระแสไหลผ่านแอมมิเตอร์นั่นเอง
4.3 โอห์มมิเตอร์แบบโพเทนชิโอมิเตอร์ (Potentiometer)
เป็นโอห์มมิเตอร์แบบหนึ่งที่นิยมใช้กันมากในมัลติมิเตอร์ทั่วๆ ไป ลักษณะของวงจรเบื้องต้นแสดงดังรูปที่ 2.16
จากสมการ (5) จะเห็นว่า ถ้า Rx มีค่าเป็นศูนย์ จะให้กระแสที่ผ่านแอมมิเตอร์เป็นศูนย์ ถ้า Rx มีค่าสูง Infinite ก็จะมีกระแสไหลผ่านแอมมิเตอร์นั่นเอง
4.3 โอห์มมิเตอร์แบบโพเทนชิโอมิเตอร์ (Potentiometer)
เป็นโอห์มมิเตอร์แบบหนึ่งที่นิยมใช้กันมากในมัลติมิเตอร์ทั่วๆ ไป ลักษณะของวงจรเบื้องต้นแสดงดังรูปที่ 2.16
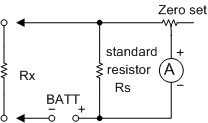 รูปที่ 2.16 แสดงโอห์มมิเตอร์แบบ Potentiometer
จากรูปที่ 2.16 จะเห็นว่า วงจรแอมมิเตอร์หรือมิเตอร์มูฟเม้นท์กับความต้านทานปรับค่าได้ จะต่อขนานกับตัวต้านทานค่ามาตรฐานค่าหนึ่ง (Rs) เมื่อนำสายวัดทั้งสอง
มาแตะกันเพื่อปรับค่า Zero set นั้น วงจรมิเตอร์มูฟเม้นท์จะต้องแสดงค่าของแรงไฟแบตเตอรี่นั้น เพราะลักษณะของ วงจรมิเตอร์มูฟเม้นท์และความต้านทาน Zero set จะต่ออนุกรม
เป็นวงจรโวลท์มิเตอร์ นั่นเอง ในขณะนี้เราก็สามารถปรับค่าความต้านทาน Zero set เพื่อให้เข็มมิเตอร์ชี้เต็มสเกล ซึ่งแสดงค่าความต้านทานเป็นศูนย์โอห์มนั่นเอง และเมื่อนำสายวัด
มาต่อกับตัวต้านทานที่จะวัด (Rx) ก็จะทำให้กระแสไหลผ่านวงจรมิเตอร์มูฟเม้นท์น้อยลงไปเรื่อยๆ จนถึงค่า Rx เป็นค่า Infinite โอห์มก็จะไม่มีกระแสผ่านวงจรมิเตอร์มูฟเม้นท์เลย
ดังนั้นลักษณะสเกลของโอห์มมิเตอร์ชนิดนี้จึงเป็นแบบกลับหรือเรีกว่า Back of Scale เหมือนกับโอห์มมิเตอร์แบบอนุกรม
รูปที่ 2.16 แสดงโอห์มมิเตอร์แบบ Potentiometer
จากรูปที่ 2.16 จะเห็นว่า วงจรแอมมิเตอร์หรือมิเตอร์มูฟเม้นท์กับความต้านทานปรับค่าได้ จะต่อขนานกับตัวต้านทานค่ามาตรฐานค่าหนึ่ง (Rs) เมื่อนำสายวัดทั้งสอง
มาแตะกันเพื่อปรับค่า Zero set นั้น วงจรมิเตอร์มูฟเม้นท์จะต้องแสดงค่าของแรงไฟแบตเตอรี่นั้น เพราะลักษณะของ วงจรมิเตอร์มูฟเม้นท์และความต้านทาน Zero set จะต่ออนุกรม
เป็นวงจรโวลท์มิเตอร์ นั่นเอง ในขณะนี้เราก็สามารถปรับค่าความต้านทาน Zero set เพื่อให้เข็มมิเตอร์ชี้เต็มสเกล ซึ่งแสดงค่าความต้านทานเป็นศูนย์โอห์มนั่นเอง และเมื่อนำสายวัด
มาต่อกับตัวต้านทานที่จะวัด (Rx) ก็จะทำให้กระแสไหลผ่านวงจรมิเตอร์มูฟเม้นท์น้อยลงไปเรื่อยๆ จนถึงค่า Rx เป็นค่า Infinite โอห์มก็จะไม่มีกระแสผ่านวงจรมิเตอร์มูฟเม้นท์เลย
ดังนั้นลักษณะสเกลของโอห์มมิเตอร์ชนิดนี้จึงเป็นแบบกลับหรือเรีกว่า Back of Scale เหมือนกับโอห์มมิเตอร์แบบอนุกรม
วงจรมิเตอร์มูฟเม้นท์และความต้านทาน Zero set ที่ต่อขนานกับความต้านทานค่ามาตรฐานนั้น วงจรมิเตอร์จะต้องมีค่าความต้านทานสูงมากเมื่อเทียบกับความต้าน
ทานมาตรฐาน จึงทำให้ความต้านทานมาตรฐานนี้เป็นตัวกำหนดค่าความต้านทานรวมของโอห์มิเตอร์นี้ และค่าความต้านทานมาตรฐานนี้ก็จะเป็นตัวกำหนดค่าตัวต้านทานกลางสเกล
ของโอห์มมิเตอร์ดังนั้นถ้าเปลี่ยนค่าความต้านทานมาตรฐานเพิ่มขึ้นเป็น 10 เท่า สเกลของโอห์มมิเตอร์เดิมก็จะอ่านค่าความต้านทานได้เป็น 10 เท่าด้วย
 รูปที่ 2.17 แสดงตัวอย่างวงจรโอห์มมิเตอร์แบบ Potentiometer ในทางปฏิบัติ
จากรูป 2.17 เป็นตัวอย่างวงจรโอห์มมิเตอร์แบบ Potentiometer ในทางปฏิบัติจากมิลติมิเตอร์ซิมสันรุ่น 260 ( Simpson Model 260 ) ที่สามารถวัดค่าความต้านทาน
ได้ 3 ย่านวัด คือ Rx1, Rx100 และ Rx10K ในย่านต่ำสุดคือ Rx1 ค่าความต้านทานมาตรฐานคือ 11.5W ที่ย่าน Rx100 ค่าความต้านทานมาตรฐานคือ 1138W รวมกับ 11.5W รวมเป็น
1148.5W หรือประมาณ 100 เท่า ของย่าน Rx1 แต่ในย่าน Rx10K นั้นค่าความต้านทานมาตรฐานควรจะเป็น 115000W หรือ 10,000 เท่า ของค่าความต้านทานมาตรฐานย่าน Rx1 แต่
ในวงจรไม่เป็นเช่นนั้นเพราะว่า ถ้าใช้มาตรฐาน 115000W ต่อขนานกับมิเตอร์มูฟเม้นท์แล้วนำไปอนุกรมกับแบตเตอรี่ 1.5V นำมาวัดตัวต้านทาน Rx ค่า 115000W จะเห็นว่าค่ากระแสที่
ไหลผ่านมิเตอร์มูฟเม้นท์ไม่ถึงครึ่งหนึ่งคือ 25uA (มิเตอร์มูฟเม้นท์ขนาด 50uA, 2K) จะมีเพียง 14uA เท่านั้นจึงทำให้เข็มของมิเตอร์ชี้ไม่ถึงค่ากลางสเกล เพราะฉะนั้นในทางปฏิบัติจึงใช้
วิธีการเพิ่มแรงดันแบตเตอรี่ให้สูงขึ้นเป็น 7.5V และแรงไฟแบตเตอรี่ที่เพิ่มขึ้นมานี้ไม่ได้ตกคร่อมความต้านทานมาตรฐานเลยทีเดียว เพราะถ้าทำเช่นนั้นก็จะต้องทำการเปลี่ยนวงจรทาง
ด้านมิเตอร์มูฟเม้นท์และความต้านทาน Zero set กันใหม่เนื่องจากแรงไฟตกคร่อมสูงเกินไป
4.3.1 การวิเคราะห์วงจรโอห์มมิเตอร์ ในการวิเคราะห์นี้เราจะคำนวณหาค่ากระแสที่ผ่านมิเตอร์มูฟเม้นท์และใน ย่านต่างๆ คือ ย่าน Rx1, Rx100 และ Rx10KWตามลำ
ดับ จากรูปที่2.16 โดยพิจารณาทีละย่านดังนี้
พิจารณาย่านวัด Rx1
ในย่านนี้ เมื่อนำมาเขียนเป็นวงจรย่านนี้ย่านเดียว จะได้ดังรูปที่ 2.18
รูปที่ 2.17 แสดงตัวอย่างวงจรโอห์มมิเตอร์แบบ Potentiometer ในทางปฏิบัติ
จากรูป 2.17 เป็นตัวอย่างวงจรโอห์มมิเตอร์แบบ Potentiometer ในทางปฏิบัติจากมิลติมิเตอร์ซิมสันรุ่น 260 ( Simpson Model 260 ) ที่สามารถวัดค่าความต้านทาน
ได้ 3 ย่านวัด คือ Rx1, Rx100 และ Rx10K ในย่านต่ำสุดคือ Rx1 ค่าความต้านทานมาตรฐานคือ 11.5W ที่ย่าน Rx100 ค่าความต้านทานมาตรฐานคือ 1138W รวมกับ 11.5W รวมเป็น
1148.5W หรือประมาณ 100 เท่า ของย่าน Rx1 แต่ในย่าน Rx10K นั้นค่าความต้านทานมาตรฐานควรจะเป็น 115000W หรือ 10,000 เท่า ของค่าความต้านทานมาตรฐานย่าน Rx1 แต่
ในวงจรไม่เป็นเช่นนั้นเพราะว่า ถ้าใช้มาตรฐาน 115000W ต่อขนานกับมิเตอร์มูฟเม้นท์แล้วนำไปอนุกรมกับแบตเตอรี่ 1.5V นำมาวัดตัวต้านทาน Rx ค่า 115000W จะเห็นว่าค่ากระแสที่
ไหลผ่านมิเตอร์มูฟเม้นท์ไม่ถึงครึ่งหนึ่งคือ 25uA (มิเตอร์มูฟเม้นท์ขนาด 50uA, 2K) จะมีเพียง 14uA เท่านั้นจึงทำให้เข็มของมิเตอร์ชี้ไม่ถึงค่ากลางสเกล เพราะฉะนั้นในทางปฏิบัติจึงใช้
วิธีการเพิ่มแรงดันแบตเตอรี่ให้สูงขึ้นเป็น 7.5V และแรงไฟแบตเตอรี่ที่เพิ่มขึ้นมานี้ไม่ได้ตกคร่อมความต้านทานมาตรฐานเลยทีเดียว เพราะถ้าทำเช่นนั้นก็จะต้องทำการเปลี่ยนวงจรทาง
ด้านมิเตอร์มูฟเม้นท์และความต้านทาน Zero set กันใหม่เนื่องจากแรงไฟตกคร่อมสูงเกินไป
4.3.1 การวิเคราะห์วงจรโอห์มมิเตอร์ ในการวิเคราะห์นี้เราจะคำนวณหาค่ากระแสที่ผ่านมิเตอร์มูฟเม้นท์และใน ย่านต่างๆ คือ ย่าน Rx1, Rx100 และ Rx10KWตามลำ
ดับ จากรูปที่2.16 โดยพิจารณาทีละย่านดังนี้
พิจารณาย่านวัด Rx1
ในย่านนี้ เมื่อนำมาเขียนเป็นวงจรย่านนี้ย่านเดียว จะได้ดังรูปที่ 2.18
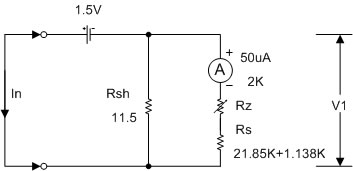 รูปที่ 2.18 แสดงวงจรโอห์มมิเตอร์ย่าน Rx1
จากรูปที่ 2.18 เมื่อนำสายวัดมาแตะกัน แล้วปรับความต้านทาน Rz ให้เข็มมิเตอร์ชี้เต็มสเกลที่ศูนย์โอห์ม จะได้ว่า
รูปที่ 2.18 แสดงวงจรโอห์มมิเตอร์ย่าน Rx1
จากรูปที่ 2.18 เมื่อนำสายวัดมาแตะกัน แล้วปรับความต้านทาน Rz ให้เข็มมิเตอร์ชี้เต็มสเกลที่ศูนย์โอห์ม จะได้ว่า
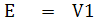

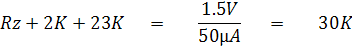
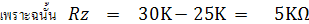
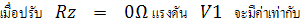
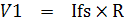
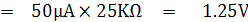 แสดงว่าเมื่อปรับ Rz = 0W เข็มมิเตอร์จะชี้เต็มสเกลได้ต้องมีแรงไฟจากแบตเตอรี่ค่าต่ำสุด 1.25V และเมื่อปรับ Rz = 10KW แรงดัน V1 จะมีค่าเท่ากับ
แสดงว่าเมื่อปรับ Rz = 0W เข็มมิเตอร์จะชี้เต็มสเกลได้ต้องมีแรงไฟจากแบตเตอรี่ค่าต่ำสุด 1.25V และเมื่อปรับ Rz = 10KW แรงดัน V1 จะมีค่าเท่ากับ

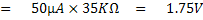 แสดงว่าเมื่อปรับ Rz = 10KW เข็มมิเตอร์จะชี้เต็มสเกลได้ต้องมีแรงไฟจากแบตเตอรี่ค่าต่ำสุด 1.75V
สรุปได้ว่า ค่า Rz ที่ปรับค่าได้ในวงจรโอห์มมิเตอร์ย่านวัด Rx1 นี้จะสามารถปรับเข็มชี้เต็มสเกลได้ (Zero Ohm) ได้ โดยที่แรงไฟจากแบตเตอรี่ระหว่าง 1.25V ถึง 1.75V
เปลี่ยนแปลงจาก 1.5V ในวงจร เท่ากับ + 0.25V
ที่ Rz = 0W ค่าความต้านทานภายในของโอห์มิเตอร์ย่านนี้ จะเท่ากับ
แสดงว่าเมื่อปรับ Rz = 10KW เข็มมิเตอร์จะชี้เต็มสเกลได้ต้องมีแรงไฟจากแบตเตอรี่ค่าต่ำสุด 1.75V
สรุปได้ว่า ค่า Rz ที่ปรับค่าได้ในวงจรโอห์มมิเตอร์ย่านวัด Rx1 นี้จะสามารถปรับเข็มชี้เต็มสเกลได้ (Zero Ohm) ได้ โดยที่แรงไฟจากแบตเตอรี่ระหว่าง 1.25V ถึง 1.75V
เปลี่ยนแปลงจาก 1.5V ในวงจร เท่ากับ + 0.25V
ที่ Rz = 0W ค่าความต้านทานภายในของโอห์มิเตอร์ย่านนี้ จะเท่ากับ
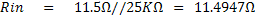 ที่ Rz = 10KW ค่าความต้านทานภายในของโอห์มิเตอร์ย่านนี้ จะเท่ากับ
ที่ Rz = 10KW ค่าความต้านทานภายในของโอห์มิเตอร์ย่านนี้ จะเท่ากับ
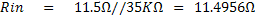 เพราะฉะนั้นค่าความต้านทานภายในรวมเฉลี่ยแล้วจะมีค่าเท่ากับ 11.495W หรือประมาณ 11.5W และค่ากระแสที่ไหลผ่านสายวัดที่แตะกัน จะมีค่าเท่ากับ In คือ
เพราะฉะนั้นค่าความต้านทานภายในรวมเฉลี่ยแล้วจะมีค่าเท่ากับ 11.495W หรือประมาณ 11.5W และค่ากระแสที่ไหลผ่านสายวัดที่แตะกัน จะมีค่าเท่ากับ In คือ
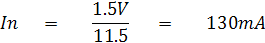 และเมื่อนำค่าความต้านทาน Rx เท่ากับ 12W มาต่อวัด จะได้ดังรูปที่ 2.18
และเมื่อนำค่าความต้านทาน Rx เท่ากับ 12W มาต่อวัด จะได้ดังรูปที่ 2.18
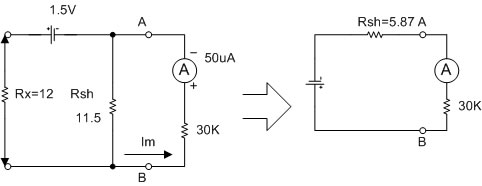 ก) เมื่อวัดตัวต้านทาน Rx = 12W ข) Thevenin Equivalent Circuit
รูปที่ 2.19 แสดงวงจรฌอห์มมิเตอร์ย่าน Rx1 ขณะวัดตัวต้านทาน Rx
ก) เมื่อวัดตัวต้านทาน Rx = 12W ข) Thevenin Equivalent Circuit
รูปที่ 2.19 แสดงวงจรฌอห์มมิเตอร์ย่าน Rx1 ขณะวัดตัวต้านทาน Rx
 หา Thevenin Equivalent Circuit สำหรับส่วนของวงจรที่จุด A-B จะได้
หา Thevenin Equivalent Circuit สำหรับส่วนของวงจรที่จุด A-B จะได้
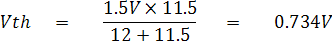
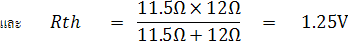 เพราะฉะนั้นค่ากระแสที่ไหลผ่านมิเตอร์มูฟเม้นท์ หาจากวงจร Thevenin Equivalent Circuit ดังรูป ข)
เพราะฉะนั้นค่ากระแสที่ไหลผ่านมิเตอร์มูฟเม้นท์ หาจากวงจร Thevenin Equivalent Circuit ดังรูป ข)
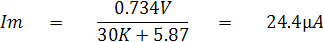 ในทางปฏิบัติจะถือว่า ค่า Im มีค่าประมาณ 25uA นั่นเอง เนื่องจากการคำนวณไม่ได้คิดค่าความต้านทานภายในของแบตเตอรี่ด้วย
พิจารณาย่านวัด R x 100
ในย่านวัด Rx100 เมื่อนำมาเขียนใหม่จะได้ดังรูปที่ 2.20
ในทางปฏิบัติจะถือว่า ค่า Im มีค่าประมาณ 25uA นั่นเอง เนื่องจากการคำนวณไม่ได้คิดค่าความต้านทานภายในของแบตเตอรี่ด้วย
พิจารณาย่านวัด R x 100
ในย่านวัด Rx100 เมื่อนำมาเขียนใหม่จะได้ดังรูปที่ 2.20
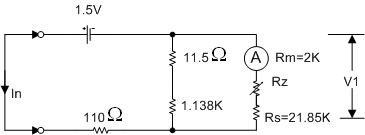 รูปที่ 2.20 แสดงวงจรโอห์มมิเตอร์ ย่าน R x 100
จากรูปที่ 2.20 เมื่อนำสายวัดทั้งสองมาแตะกันแล้วปรับ Rz เพื่อทำการ Zero set จะเห็นว่าขณะนี้ค่าความต้านทานภายในของโอห์มมิเตอร์จะมีค่าประมาณหรือ
เท่ากับ ค่าความต้านทานกลางสเกลย่าน Rx100 คือ 1.2KW ดังนั้นค่ากระแสในวงจรจะเท่ากับ
รูปที่ 2.20 แสดงวงจรโอห์มมิเตอร์ ย่าน R x 100
จากรูปที่ 2.20 เมื่อนำสายวัดทั้งสองมาแตะกันแล้วปรับ Rz เพื่อทำการ Zero set จะเห็นว่าขณะนี้ค่าความต้านทานภายในของโอห์มมิเตอร์จะมีค่าประมาณหรือ
เท่ากับ ค่าความต้านทานกลางสเกลย่าน Rx100 คือ 1.2KW ดังนั้นค่ากระแสในวงจรจะเท่ากับ
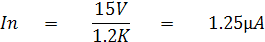
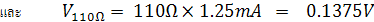 เพราะฉะนั้น
เพราะฉะนั้น
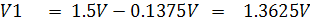
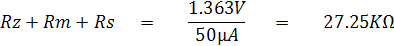

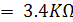 เมื่อนำ Rx ค่ากลางสเกลคือ 1.2KW มาวัดวงจรจะเป็นดังรูปที่ 2.21
เมื่อนำ Rx ค่ากลางสเกลคือ 1.2KW มาวัดวงจรจะเป็นดังรูปที่ 2.21
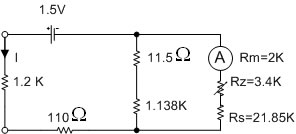 รูปที่ 2.21 แสดงวงจรโอห์มมิเตอร์ ย่าน Rx100 เมื่อวัด Rx ค่า 1.2KW
จากรูปที่ 2.21 คำนวณหากระแสที่ไหลผ่าน มูฟเม้นท์มิเตอร์ โดยวิธี Current Divider
รูปที่ 2.21 แสดงวงจรโอห์มมิเตอร์ ย่าน Rx100 เมื่อวัด Rx ค่า 1.2KW
จากรูปที่ 2.21 คำนวณหากระแสที่ไหลผ่าน มูฟเม้นท์มิเตอร์ โดยวิธี Current Divider
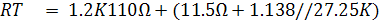
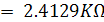
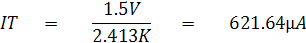 จาก Current Divider Rule
จาก Current Divider Rule
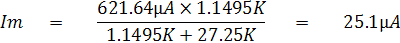 ในทางปฏิบัติ Im ก็คือกระแสที่ทำให้เข็มมิเตอร์ชี้ขึ้นกลางสเกลนั่นเอง
พิจารณาย่าน R x 10 K
ในย่านวัด R x 10K เมื่อนำมาเขียนใหม่จะได้ดังรูปที่ 2.22
ในทางปฏิบัติ Im ก็คือกระแสที่ทำให้เข็มมิเตอร์ชี้ขึ้นกลางสเกลนั่นเอง
พิจารณาย่าน R x 10 K
ในย่านวัด R x 10K เมื่อนำมาเขียนใหม่จะได้ดังรูปที่ 2.22
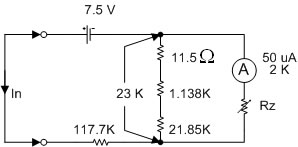 รูปที่ 2.22 แสดงโอห์มมิเตอร์ย่าน Rx10K
รูปที่ 2.22 แสดงโอห์มมิเตอร์ย่าน Rx10K
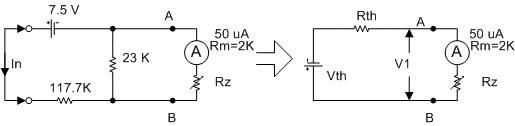 รูปที่ 2.23 แสดง Thevenin equivalent circuit ย่าน Rx10K
จากรูปที่ 2.23 ค่า Vth และ Rth หาได้ดังนี้
รูปที่ 2.23 แสดง Thevenin equivalent circuit ย่าน Rx10K
จากรูปที่ 2.23 ค่า Vth และ Rth หาได้ดังนี้
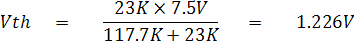
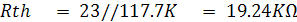 และเมื่อปรับ Rz ให้กระแสเต็มสเกลจะได้
และเมื่อปรับ Rz ให้กระแสเต็มสเกลจะได้
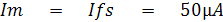
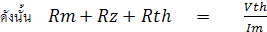
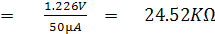
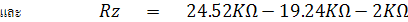
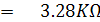 เมื่อนำ Rx ค่ากลางสเกลคือ 120 KW มาวัดกระแสที่ไหลผ่านมิเตอร์มูฟเม้นท์จะได้ดังนี้
เมื่อนำ Rx ค่ากลางสเกลคือ 120 KW มาวัดกระแสที่ไหลผ่านมิเตอร์มูฟเม้นท์จะได้ดังนี้
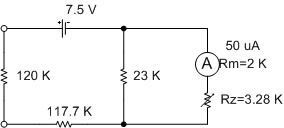 รูปที่ 2.24 แสดงย่านวัด Rx10K เมื่อวัดค่า Rx ค่า 120KW
จากรูปที่ 2.24 จะได้ว่า
รูปที่ 2.24 แสดงย่านวัด Rx10K เมื่อวัดค่า Rx ค่า 120KW
จากรูปที่ 2.24 จะได้ว่า
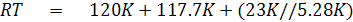
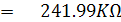
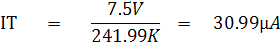 จาก Current Divider Rule
จาก Current Divider Rule
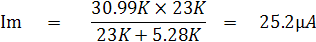 ในทางปฏิบัติคือ ค่ากระแสกลางสเกลนั่นเอง
4.4 การออกแบบวงจรโอห์มมิเตอร์
ผลจากการวิเคราะห์วงจรโอห์มมิเตอร์ของมัลติมิเตอร์ ซิมสัน 260 จะเห็นว่าลักษณะวงจรเป็นโอห์มมิเตอร์แบบ Potentio meter ค่าความต้านทานกลางสเกลคือ 12W,
1.2 KW และ 120KW สำหรับย่าน Rx1, Rx100 และ Rx10KW ตามลำดับ ค่าความต้านทานกลางสเกลนี้จะเป็นตัวกำหนดค่ากระแสที่ขั้ววัดขณะที่ทำการ Zero set ย่าน Rx1 และ
Rx100 ใช้แบตเตอรี่ 1.5V ส่วนย่าน Rx10K ใช้แบตเตอรี่ 7.5V กระแสเมื่อทำการปรับ Zero set แล้วในแต่ละย่านคือ 125mA สำหรับย่าน Rx1, 1.25mA สำหรับย่าน Rx100 และ
62.5uA สำหรับย่าน Rx10K
ในทางปฏิบัติคือ ค่ากระแสกลางสเกลนั่นเอง
4.4 การออกแบบวงจรโอห์มมิเตอร์
ผลจากการวิเคราะห์วงจรโอห์มมิเตอร์ของมัลติมิเตอร์ ซิมสัน 260 จะเห็นว่าลักษณะวงจรเป็นโอห์มมิเตอร์แบบ Potentio meter ค่าความต้านทานกลางสเกลคือ 12W,
1.2 KW และ 120KW สำหรับย่าน Rx1, Rx100 และ Rx10KW ตามลำดับ ค่าความต้านทานกลางสเกลนี้จะเป็นตัวกำหนดค่ากระแสที่ขั้ววัดขณะที่ทำการ Zero set ย่าน Rx1 และ
Rx100 ใช้แบตเตอรี่ 1.5V ส่วนย่าน Rx10K ใช้แบตเตอรี่ 7.5V กระแสเมื่อทำการปรับ Zero set แล้วในแต่ละย่านคือ 125mA สำหรับย่าน Rx1, 1.25mA สำหรับย่าน Rx100 และ
62.5uA สำหรับย่าน Rx10K
ในการออกแบบนั้นเราจะต้องกำหนดค่าความต้านทานกลางสเกล ในย่าน Rx1 แล้วเลือกมิเตอร์มูฟเม้นท์ที่จะใช้ รวมทั้งตัวต้านทานที่ปรับค่าได้ที่ใช้สำหรับ Zero set
และย่านที่ต้องการ เช่น ถ้าต้องการออกแบบโอห์มมิเตอร์ตามตัวอย่างที่วิเคราะห์มาก็คือ ต้องการย่านวัด 3 ย่านวัดคือ Rx1, Rx100 และ Rx 10K ค่าความต้านทานกลางสเกล 12W
ตัวต้านทานปรับค่าได้ (Rz) คือ 10KW ใช้มิเตอร์มูฟเม้นท์ขนาด 50uA ความต้านทานภายใน 2KW
เมื่อเราทราบความต้องการและสิ่งที่กำหนดให้แล้วเราจะทำการคำนวณหาค่าแรงเคลื่อนหรือแบตเตอรี่ที่จะใช้ในแต่ละย่านวัด โดยคำนึงว่าเมื่อทำการลัดวงจรที่สายวัด
(Zero set) จะต้องจ่ายกระแสออกมาได้ไม่ต่ำกว่ากระแสเต็มสเกลของมิเตอร์มูฟเม้นท์ที่เลือกใช้ โดยเราสามารถเขียน วงจรโอห์มมิเตอร์ในการออกแบบใหม่ได้ดังรูปที่ 2.24
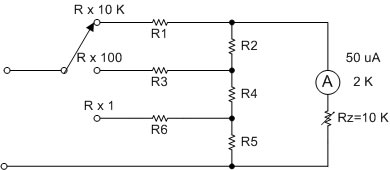 รูปที่ 2.25 แสดงวงจรโอห์มมิเตอร์ที่จะออกแบบ
คำนวณหาคาแรงเคลื่อนเพื่อเลือกใช้แบตเตอรี่ในแต่ละย่านวัด
รูปที่ 2.25 แสดงวงจรโอห์มมิเตอร์ที่จะออกแบบ
คำนวณหาคาแรงเคลื่อนเพื่อเลือกใช้แบตเตอรี่ในแต่ละย่านวัด
ในย่าน R x 1 ค่าความต้านทานของวงจรในย่านนี้จะมีค่าเท่ากับค่าความต้านทานกลางสเกล คือ 12W ดังนั้นถ้ากำหนดแรงเคลื่อนเท่ากับ 1.5V กระแสที่จ่ายออกมา
จะมีค่าเท่ากับ
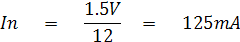 จะะเห็นว่าเมื่อลัดวงจรเพื่อปรับ Zero set จะสามารถจ่ายกระแสได้ 125mA ซึ่งมีค่ามากกว่ากระแสเต็มสเกลของมิเตอร์มูฟเม้นท์คือ 50uA ดังนั้นจึงเลือกค่าแบตเตอรี่
ที่จะใช้ในย่านนี้คือ 1.5V และสำหรับในย่านอื่นๆ ก็จะใช้หลักการเดียวกันนี้ คือ
ในย่าน R x 100 ค่าความต้านทานของวงจรในย่านนี้จะมีค่าเท่ากับค่าความต้านทานกลางสเกล คือ 1.2KW เลือกแบตเตอรี่ 1.5V เพราะสามารถจ่ายกระแสได้
มากกว่ากระแสเต็มสเกลของมิเตอร์มูฟเม้นท์คือ 50uA คือ
จะะเห็นว่าเมื่อลัดวงจรเพื่อปรับ Zero set จะสามารถจ่ายกระแสได้ 125mA ซึ่งมีค่ามากกว่ากระแสเต็มสเกลของมิเตอร์มูฟเม้นท์คือ 50uA ดังนั้นจึงเลือกค่าแบตเตอรี่
ที่จะใช้ในย่านนี้คือ 1.5V และสำหรับในย่านอื่นๆ ก็จะใช้หลักการเดียวกันนี้ คือ
ในย่าน R x 100 ค่าความต้านทานของวงจรในย่านนี้จะมีค่าเท่ากับค่าความต้านทานกลางสเกล คือ 1.2KW เลือกแบตเตอรี่ 1.5V เพราะสามารถจ่ายกระแสได้
มากกว่ากระแสเต็มสเกลของมิเตอร์มูฟเม้นท์คือ 50uA คือ
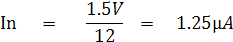 ในย่าน R x 10 K ค่าความต้านทานของวงจรในย่านนี้จะมีค่าเท่ากับค่าความต้านทานกลางสเกล คือ 120KW เลือกแบตเตอรี่ 7.5V เพราะสามารถจ่ายกระแสได้
มากกว่ากระแสเต็มสเกลของมิเตอร์มูฟเม้นท์คือ 50uA คือ
ในย่าน R x 10 K ค่าความต้านทานของวงจรในย่านนี้จะมีค่าเท่ากับค่าความต้านทานกลางสเกล คือ 120KW เลือกแบตเตอรี่ 7.5V เพราะสามารถจ่ายกระแสได้
มากกว่ากระแสเต็มสเกลของมิเตอร์มูฟเม้นท์คือ 50uA คือ
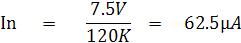 ดังนั้นเลือกแบตเตอรี่ในแต่ละย่านวัดดังนี้
ดังนั้นเลือกแบตเตอรี่ในแต่ละย่านวัดดังนี้
R x 1 เลือกแบตเตอรี่ 1.5 V
R x 100 เลือกแบตเตอรี่ 1.5 V
R x 10 K เลือกแบตเตอรี่ 7.5 V
!คำนวณหาค่าตัวต้านทานในแต่ละย่านดังนี้
ย่าน R x 10 K
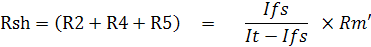 Ifs คือกระแสเต็มสเกลของมิเตอร์มูฟเม้นท์ = 50uA
Ifs คือกระแสเต็มสเกลของมิเตอร์มูฟเม้นท์ = 50uA
It คือ กระแสขณะลัดวงจรที่สายวัดทั้งสอง = 62.5uA
Rm' คือความต้านทานภายในมูฟเม้นท์รวมกับความต้านทาน Rz (Rm + Rz) หาได้จาก
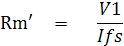 V1 คือแรงดันตกคร่อม Rm+Rz ขณะปรับ Zero set หาได้จากการคำนวณหาแรงดัน ตกคร่อม Rm + Rz ขณะที่ Rz ปรับค่าต่ำสุดเท่ากับ 0W
และแรงดันตกคร่อม Rm + Rz ขณะที่ Rz ปรับค่าสูงสุดเท่ากับ 10KW แล้วเลือกค่าที่อยู่ในช่วงการปรับ Rz ระหว่าง 0-10KW ดังนี้
เมื่อปรับ Rz = 0W แรงดันตกคร่อมที่ Rm + Rz ที่ทำให้เกิดกระแสเต็มสเกลของมิเตอร์มูฟเม้นท์คือ
V1 คือแรงดันตกคร่อม Rm+Rz ขณะปรับ Zero set หาได้จากการคำนวณหาแรงดัน ตกคร่อม Rm + Rz ขณะที่ Rz ปรับค่าต่ำสุดเท่ากับ 0W
และแรงดันตกคร่อม Rm + Rz ขณะที่ Rz ปรับค่าสูงสุดเท่ากับ 10KW แล้วเลือกค่าที่อยู่ในช่วงการปรับ Rz ระหว่าง 0-10KW ดังนี้
เมื่อปรับ Rz = 0W แรงดันตกคร่อมที่ Rm + Rz ที่ทำให้เกิดกระแสเต็มสเกลของมิเตอร์มูฟเม้นท์คือ
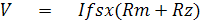
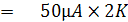
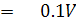 เมื่อปรับ Rz = 10KW แรงดันตกคร่อมที่ Rm + Rz ที่ทำให้เกิดกระแสเต็มสเกลของมิเตอร์มูฟเม้นท์คือ
เมื่อปรับ Rz = 10KW แรงดันตกคร่อมที่ Rm + Rz ที่ทำให้เกิดกระแสเต็มสเกลของมิเตอร์มูฟเม้นท์คือ
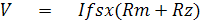
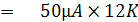
 ที่บนสเกล Dc Voltmeter จะเห็นว่าค่าแรงไฟสูงสุดที่เต็มสเกลจะสามารถวัดได้ตั้งแต่ 0.25V ขึ้นไป นั่นคือแรงดัน V1 ควรอยู่ในย่าน 0.25 V ขึ้นไป ในที่นี้ถ้า
เลือกค่า V1 ที่ตกคร่อมมิเตอร์ให้สูงกว่าค่าสูงสุดที่ปลายสเกลของ DC Voltmeter อีกประมาณ 15% จะได้ค่าแรงไฟ V1 ประมาณ
ที่บนสเกล Dc Voltmeter จะเห็นว่าค่าแรงไฟสูงสุดที่เต็มสเกลจะสามารถวัดได้ตั้งแต่ 0.25V ขึ้นไป นั่นคือแรงดัน V1 ควรอยู่ในย่าน 0.25 V ขึ้นไป ในที่นี้ถ้า
เลือกค่า V1 ที่ตกคร่อมมิเตอร์ให้สูงกว่าค่าสูงสุดที่ปลายสเกลของ DC Voltmeter อีกประมาณ 15% จะได้ค่าแรงไฟ V1 ประมาณ
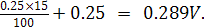 ดังนั้นจะสามารถคำนวณหาค่า Rz ขณะ Zero set ได้
ดังนั้นจะสามารถคำนวณหาค่า Rz ขณะ Zero set ได้
 จาก Rm' = Rm + Rz เพราะฉะนั้น Rz หาได้จาก
จาก Rm' = Rm + Rz เพราะฉะนั้น Rz หาได้จาก
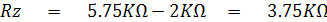
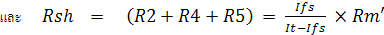
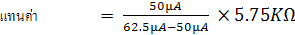

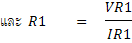
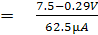
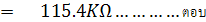 ย่าน R x 100
จากสูตรการคำนวณความต้านทานแบบ Ayrton Shunt จะได้
ย่าน R x 100
จากสูตรการคำนวณความต้านทานแบบ Ayrton Shunt จะได้
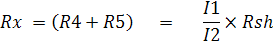
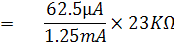
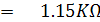
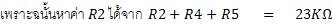
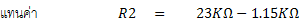
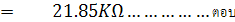
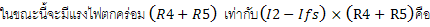
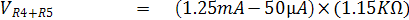
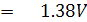
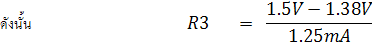
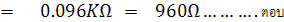 ย่าน R x 1
จากสูตรการคำนวณความต้านทานแบบ Ayrton Shunt จะได้
ย่าน R x 1
จากสูตรการคำนวณความต้านทานแบบ Ayrton Shunt จะได้

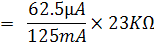
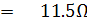
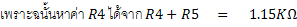
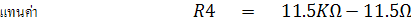
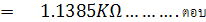
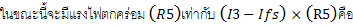
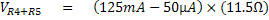
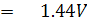
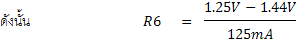
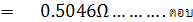 ความต้านทาน R6 มีค่าน้อยมากอาจตัดทิ้งได้ เพราะในทางปฏิบัติจะมีความต้านทานภายในแบตเตอรี่และสายต่อวงจรมาเกี่ยวข้องด้วย
ความต้านทาน R6 มีค่าน้อยมากอาจตัดทิ้งได้ เพราะในทางปฏิบัติจะมีความต้านทานภายในแบตเตอรี่และสายต่อวงจรมาเกี่ยวข้องด้วย
ซึ่งวงจรที่ออกแบบได้เราสามารถเขียนเป็นวงจรที่สมบูรณ์ได้ดังรูปที่ 2.26
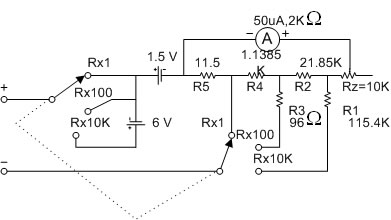 รูปที่ 2.26 แสดงวงจรโอห์มมิเตอร์แบบ Potentio-meter ที่ออกแบบ
รูปที่ 2.26 แสดงวงจรโอห์มมิเตอร์แบบ Potentio-meter ที่ออกแบบ
 รูปที่ 2.13 แสดงวงจรโอห์มมิเตอร์อย่างง่าย
Ro คือ Thevenin Resistance ของโอห์มมิเตอร์ รวมทั้งความต้านทานในของแอมมิเตอร์ Vth คือ ค่า Open Circuit Voltage ของโอห์มมิเตอร์ที่ขั้ววัด
A – B โดยทั่วไป Ro จะเป็นตัวต้านทานชนิดปรับค่าได้ เพื่อคอยปรับให้เข็มของมิเตอร์ชี้ที่ค่าศูนย์โอห์มเสมอเมื่อลัดวงจร (Short) สาย A – B เข้าด้วยกัน ซึ่ง Ro จะปรับให้กระแส
ไหลผ่านแอมมิเตอร์เต็มสเกลพอดี ดังสมการต่อไปนี้
เมื่อ Short สาย A - B
รูปที่ 2.13 แสดงวงจรโอห์มมิเตอร์อย่างง่าย
Ro คือ Thevenin Resistance ของโอห์มมิเตอร์ รวมทั้งความต้านทานในของแอมมิเตอร์ Vth คือ ค่า Open Circuit Voltage ของโอห์มมิเตอร์ที่ขั้ววัด
A – B โดยทั่วไป Ro จะเป็นตัวต้านทานชนิดปรับค่าได้ เพื่อคอยปรับให้เข็มของมิเตอร์ชี้ที่ค่าศูนย์โอห์มเสมอเมื่อลัดวงจร (Short) สาย A – B เข้าด้วยกัน ซึ่ง Ro จะปรับให้กระแส
ไหลผ่านแอมมิเตอร์เต็มสเกลพอดี ดังสมการต่อไปนี้
เมื่อ Short สาย A - B
 รูปที่ 2.14 แสดงสเกลของโอห์มมิเตอร์
จากสมการที่ (3) เราสามารถสร้างสเกลโดยการหาค่า Rx ในเทอมของ D และ Ro ได้
รูปที่ 2.14 แสดงสเกลของโอห์มมิเตอร์
จากสมการที่ (3) เราสามารถสร้างสเกลโดยการหาค่า Rx ในเทอมของ D และ Ro ได้ รูปที่ 2.15 แสดง Shunt Ohmmeter Circuit
หลักการทำงานของโอห์มมิเตอร์ชนิดนี้อาศัยการแบ่งกระแสในวงจรในขณะที่สายวัดทั้งสองแตะกัน หมายถึงความต้านทานเป็น ศูนย์ กระแสจากแบตเตอรี่จะไหลผ่าน
สายวัดทั้งสองเกือบทั้งหมด เข็มของมิเตอร์ก็จะไม่ขึ้นเพราะมีกระแสไหลผ่านน้อยมาก และกระแสในวงจรจะถูกจำกัดด้วยตัวต้านทาน Zero Set และในขณะที่สายวัดทั้งสองจากกัน
(ความต้านทาน Rx มีค่าสูง Infinite) กระแสจากแบตเตอรี่จะไหลผ่านแอมมิเตอร์ทั้งหมด เข็มของมิเตอร์ก็จะขึ้นเต็มสเกล ฉะนั้นโอห์มมิเตอร์แบบนี้จึงมีสเกลศูนย์โอห์มอยู่ทางซ้ายมือ
และค่าความต้านทานสูงถึง Infinite อยู่ทางขวามือเหมือนกับแอมมิเตอร์ทั่วไป ซึ่งจะกลับกับโอห์มมิเตอร์แบบอนุกรมในโอห์มมิเตอร์แบบอนุกรม ค่ากระแสที่ไหลในวงจรจะลดลงเมื่อ
ความต้านทานในวงจรเพิ่มมากขึ้น ซึ่งดูจากสมการ
รูปที่ 2.15 แสดง Shunt Ohmmeter Circuit
หลักการทำงานของโอห์มมิเตอร์ชนิดนี้อาศัยการแบ่งกระแสในวงจรในขณะที่สายวัดทั้งสองแตะกัน หมายถึงความต้านทานเป็น ศูนย์ กระแสจากแบตเตอรี่จะไหลผ่าน
สายวัดทั้งสองเกือบทั้งหมด เข็มของมิเตอร์ก็จะไม่ขึ้นเพราะมีกระแสไหลผ่านน้อยมาก และกระแสในวงจรจะถูกจำกัดด้วยตัวต้านทาน Zero Set และในขณะที่สายวัดทั้งสองจากกัน
(ความต้านทาน Rx มีค่าสูง Infinite) กระแสจากแบตเตอรี่จะไหลผ่านแอมมิเตอร์ทั้งหมด เข็มของมิเตอร์ก็จะขึ้นเต็มสเกล ฉะนั้นโอห์มมิเตอร์แบบนี้จึงมีสเกลศูนย์โอห์มอยู่ทางซ้ายมือ
และค่าความต้านทานสูงถึง Infinite อยู่ทางขวามือเหมือนกับแอมมิเตอร์ทั่วไป ซึ่งจะกลับกับโอห์มมิเตอร์แบบอนุกรมในโอห์มมิเตอร์แบบอนุกรม ค่ากระแสที่ไหลในวงจรจะลดลงเมื่อ
ความต้านทานในวงจรเพิ่มมากขึ้น ซึ่งดูจากสมการ
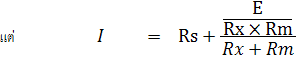
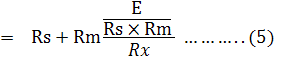 จากสมการ (5) จะเห็นว่า ถ้า Rx มีค่าเป็นศูนย์ จะให้กระแสที่ผ่านแอมมิเตอร์เป็นศูนย์ ถ้า Rx มีค่าสูง Infinite ก็จะมีกระแสไหลผ่านแอมมิเตอร์นั่นเอง
4.3 โอห์มมิเตอร์แบบโพเทนชิโอมิเตอร์ (Potentiometer)
เป็นโอห์มมิเตอร์แบบหนึ่งที่นิยมใช้กันมากในมัลติมิเตอร์ทั่วๆ ไป ลักษณะของวงจรเบื้องต้นแสดงดังรูปที่ 2.16
จากสมการ (5) จะเห็นว่า ถ้า Rx มีค่าเป็นศูนย์ จะให้กระแสที่ผ่านแอมมิเตอร์เป็นศูนย์ ถ้า Rx มีค่าสูง Infinite ก็จะมีกระแสไหลผ่านแอมมิเตอร์นั่นเอง
4.3 โอห์มมิเตอร์แบบโพเทนชิโอมิเตอร์ (Potentiometer)
เป็นโอห์มมิเตอร์แบบหนึ่งที่นิยมใช้กันมากในมัลติมิเตอร์ทั่วๆ ไป ลักษณะของวงจรเบื้องต้นแสดงดังรูปที่ 2.16
 รูปที่ 2.16 แสดงโอห์มมิเตอร์แบบ Potentiometer
จากรูปที่ 2.16 จะเห็นว่า วงจรแอมมิเตอร์หรือมิเตอร์มูฟเม้นท์กับความต้านทานปรับค่าได้ จะต่อขนานกับตัวต้านทานค่ามาตรฐานค่าหนึ่ง (Rs) เมื่อนำสายวัดทั้งสอง
มาแตะกันเพื่อปรับค่า Zero set นั้น วงจรมิเตอร์มูฟเม้นท์จะต้องแสดงค่าของแรงไฟแบตเตอรี่นั้น เพราะลักษณะของ วงจรมิเตอร์มูฟเม้นท์และความต้านทาน Zero set จะต่ออนุกรม
เป็นวงจรโวลท์มิเตอร์ นั่นเอง ในขณะนี้เราก็สามารถปรับค่าความต้านทาน Zero set เพื่อให้เข็มมิเตอร์ชี้เต็มสเกล ซึ่งแสดงค่าความต้านทานเป็นศูนย์โอห์มนั่นเอง และเมื่อนำสายวัด
มาต่อกับตัวต้านทานที่จะวัด (Rx) ก็จะทำให้กระแสไหลผ่านวงจรมิเตอร์มูฟเม้นท์น้อยลงไปเรื่อยๆ จนถึงค่า Rx เป็นค่า Infinite โอห์มก็จะไม่มีกระแสผ่านวงจรมิเตอร์มูฟเม้นท์เลย
ดังนั้นลักษณะสเกลของโอห์มมิเตอร์ชนิดนี้จึงเป็นแบบกลับหรือเรีกว่า Back of Scale เหมือนกับโอห์มมิเตอร์แบบอนุกรม
รูปที่ 2.16 แสดงโอห์มมิเตอร์แบบ Potentiometer
จากรูปที่ 2.16 จะเห็นว่า วงจรแอมมิเตอร์หรือมิเตอร์มูฟเม้นท์กับความต้านทานปรับค่าได้ จะต่อขนานกับตัวต้านทานค่ามาตรฐานค่าหนึ่ง (Rs) เมื่อนำสายวัดทั้งสอง
มาแตะกันเพื่อปรับค่า Zero set นั้น วงจรมิเตอร์มูฟเม้นท์จะต้องแสดงค่าของแรงไฟแบตเตอรี่นั้น เพราะลักษณะของ วงจรมิเตอร์มูฟเม้นท์และความต้านทาน Zero set จะต่ออนุกรม
เป็นวงจรโวลท์มิเตอร์ นั่นเอง ในขณะนี้เราก็สามารถปรับค่าความต้านทาน Zero set เพื่อให้เข็มมิเตอร์ชี้เต็มสเกล ซึ่งแสดงค่าความต้านทานเป็นศูนย์โอห์มนั่นเอง และเมื่อนำสายวัด
มาต่อกับตัวต้านทานที่จะวัด (Rx) ก็จะทำให้กระแสไหลผ่านวงจรมิเตอร์มูฟเม้นท์น้อยลงไปเรื่อยๆ จนถึงค่า Rx เป็นค่า Infinite โอห์มก็จะไม่มีกระแสผ่านวงจรมิเตอร์มูฟเม้นท์เลย
ดังนั้นลักษณะสเกลของโอห์มมิเตอร์ชนิดนี้จึงเป็นแบบกลับหรือเรีกว่า Back of Scale เหมือนกับโอห์มมิเตอร์แบบอนุกรม  รูปที่ 2.17 แสดงตัวอย่างวงจรโอห์มมิเตอร์แบบ Potentiometer ในทางปฏิบัติ
จากรูป 2.17 เป็นตัวอย่างวงจรโอห์มมิเตอร์แบบ Potentiometer ในทางปฏิบัติจากมิลติมิเตอร์ซิมสันรุ่น 260 ( Simpson Model 260 ) ที่สามารถวัดค่าความต้านทาน
ได้ 3 ย่านวัด คือ Rx1, Rx100 และ Rx10K ในย่านต่ำสุดคือ Rx1 ค่าความต้านทานมาตรฐานคือ 11.5W ที่ย่าน Rx100 ค่าความต้านทานมาตรฐานคือ 1138W รวมกับ 11.5W รวมเป็น
1148.5W หรือประมาณ 100 เท่า ของย่าน Rx1 แต่ในย่าน Rx10K นั้นค่าความต้านทานมาตรฐานควรจะเป็น 115000W หรือ 10,000 เท่า ของค่าความต้านทานมาตรฐานย่าน Rx1 แต่
ในวงจรไม่เป็นเช่นนั้นเพราะว่า ถ้าใช้มาตรฐาน 115000W ต่อขนานกับมิเตอร์มูฟเม้นท์แล้วนำไปอนุกรมกับแบตเตอรี่ 1.5V นำมาวัดตัวต้านทาน Rx ค่า 115000W จะเห็นว่าค่ากระแสที่
ไหลผ่านมิเตอร์มูฟเม้นท์ไม่ถึงครึ่งหนึ่งคือ 25uA (มิเตอร์มูฟเม้นท์ขนาด 50uA, 2K) จะมีเพียง 14uA เท่านั้นจึงทำให้เข็มของมิเตอร์ชี้ไม่ถึงค่ากลางสเกล เพราะฉะนั้นในทางปฏิบัติจึงใช้
วิธีการเพิ่มแรงดันแบตเตอรี่ให้สูงขึ้นเป็น 7.5V และแรงไฟแบตเตอรี่ที่เพิ่มขึ้นมานี้ไม่ได้ตกคร่อมความต้านทานมาตรฐานเลยทีเดียว เพราะถ้าทำเช่นนั้นก็จะต้องทำการเปลี่ยนวงจรทาง
ด้านมิเตอร์มูฟเม้นท์และความต้านทาน Zero set กันใหม่เนื่องจากแรงไฟตกคร่อมสูงเกินไป
4.3.1 การวิเคราะห์วงจรโอห์มมิเตอร์ ในการวิเคราะห์นี้เราจะคำนวณหาค่ากระแสที่ผ่านมิเตอร์มูฟเม้นท์และใน ย่านต่างๆ คือ ย่าน Rx1, Rx100 และ Rx10KWตามลำ
ดับ จากรูปที่2.16 โดยพิจารณาทีละย่านดังนี้
พิจารณาย่านวัด Rx1
ในย่านนี้ เมื่อนำมาเขียนเป็นวงจรย่านนี้ย่านเดียว จะได้ดังรูปที่ 2.18
รูปที่ 2.17 แสดงตัวอย่างวงจรโอห์มมิเตอร์แบบ Potentiometer ในทางปฏิบัติ
จากรูป 2.17 เป็นตัวอย่างวงจรโอห์มมิเตอร์แบบ Potentiometer ในทางปฏิบัติจากมิลติมิเตอร์ซิมสันรุ่น 260 ( Simpson Model 260 ) ที่สามารถวัดค่าความต้านทาน
ได้ 3 ย่านวัด คือ Rx1, Rx100 และ Rx10K ในย่านต่ำสุดคือ Rx1 ค่าความต้านทานมาตรฐานคือ 11.5W ที่ย่าน Rx100 ค่าความต้านทานมาตรฐานคือ 1138W รวมกับ 11.5W รวมเป็น
1148.5W หรือประมาณ 100 เท่า ของย่าน Rx1 แต่ในย่าน Rx10K นั้นค่าความต้านทานมาตรฐานควรจะเป็น 115000W หรือ 10,000 เท่า ของค่าความต้านทานมาตรฐานย่าน Rx1 แต่
ในวงจรไม่เป็นเช่นนั้นเพราะว่า ถ้าใช้มาตรฐาน 115000W ต่อขนานกับมิเตอร์มูฟเม้นท์แล้วนำไปอนุกรมกับแบตเตอรี่ 1.5V นำมาวัดตัวต้านทาน Rx ค่า 115000W จะเห็นว่าค่ากระแสที่
ไหลผ่านมิเตอร์มูฟเม้นท์ไม่ถึงครึ่งหนึ่งคือ 25uA (มิเตอร์มูฟเม้นท์ขนาด 50uA, 2K) จะมีเพียง 14uA เท่านั้นจึงทำให้เข็มของมิเตอร์ชี้ไม่ถึงค่ากลางสเกล เพราะฉะนั้นในทางปฏิบัติจึงใช้
วิธีการเพิ่มแรงดันแบตเตอรี่ให้สูงขึ้นเป็น 7.5V และแรงไฟแบตเตอรี่ที่เพิ่มขึ้นมานี้ไม่ได้ตกคร่อมความต้านทานมาตรฐานเลยทีเดียว เพราะถ้าทำเช่นนั้นก็จะต้องทำการเปลี่ยนวงจรทาง
ด้านมิเตอร์มูฟเม้นท์และความต้านทาน Zero set กันใหม่เนื่องจากแรงไฟตกคร่อมสูงเกินไป
4.3.1 การวิเคราะห์วงจรโอห์มมิเตอร์ ในการวิเคราะห์นี้เราจะคำนวณหาค่ากระแสที่ผ่านมิเตอร์มูฟเม้นท์และใน ย่านต่างๆ คือ ย่าน Rx1, Rx100 และ Rx10KWตามลำ
ดับ จากรูปที่2.16 โดยพิจารณาทีละย่านดังนี้
พิจารณาย่านวัด Rx1
ในย่านนี้ เมื่อนำมาเขียนเป็นวงจรย่านนี้ย่านเดียว จะได้ดังรูปที่ 2.18
 รูปที่ 2.18 แสดงวงจรโอห์มมิเตอร์ย่าน Rx1
จากรูปที่ 2.18 เมื่อนำสายวัดมาแตะกัน แล้วปรับความต้านทาน Rz ให้เข็มมิเตอร์ชี้เต็มสเกลที่ศูนย์โอห์ม จะได้ว่า
รูปที่ 2.18 แสดงวงจรโอห์มมิเตอร์ย่าน Rx1
จากรูปที่ 2.18 เมื่อนำสายวัดมาแตะกัน แล้วปรับความต้านทาน Rz ให้เข็มมิเตอร์ชี้เต็มสเกลที่ศูนย์โอห์ม จะได้ว่า
 ก) เมื่อวัดตัวต้านทาน Rx = 12W ข) Thevenin Equivalent Circuit
รูปที่ 2.19 แสดงวงจรฌอห์มมิเตอร์ย่าน Rx1 ขณะวัดตัวต้านทาน Rx
ก) เมื่อวัดตัวต้านทาน Rx = 12W ข) Thevenin Equivalent Circuit
รูปที่ 2.19 แสดงวงจรฌอห์มมิเตอร์ย่าน Rx1 ขณะวัดตัวต้านทาน Rx
 รูปที่ 2.20 แสดงวงจรโอห์มมิเตอร์ ย่าน R x 100
จากรูปที่ 2.20 เมื่อนำสายวัดทั้งสองมาแตะกันแล้วปรับ Rz เพื่อทำการ Zero set จะเห็นว่าขณะนี้ค่าความต้านทานภายในของโอห์มมิเตอร์จะมีค่าประมาณหรือ
เท่ากับ ค่าความต้านทานกลางสเกลย่าน Rx100 คือ 1.2KW ดังนั้นค่ากระแสในวงจรจะเท่ากับ
รูปที่ 2.20 แสดงวงจรโอห์มมิเตอร์ ย่าน R x 100
จากรูปที่ 2.20 เมื่อนำสายวัดทั้งสองมาแตะกันแล้วปรับ Rz เพื่อทำการ Zero set จะเห็นว่าขณะนี้ค่าความต้านทานภายในของโอห์มมิเตอร์จะมีค่าประมาณหรือ
เท่ากับ ค่าความต้านทานกลางสเกลย่าน Rx100 คือ 1.2KW ดังนั้นค่ากระแสในวงจรจะเท่ากับ
 รูปที่ 2.21 แสดงวงจรโอห์มมิเตอร์ ย่าน Rx100 เมื่อวัด Rx ค่า 1.2KW
จากรูปที่ 2.21 คำนวณหากระแสที่ไหลผ่าน มูฟเม้นท์มิเตอร์ โดยวิธี Current Divider
รูปที่ 2.21 แสดงวงจรโอห์มมิเตอร์ ย่าน Rx100 เมื่อวัด Rx ค่า 1.2KW
จากรูปที่ 2.21 คำนวณหากระแสที่ไหลผ่าน มูฟเม้นท์มิเตอร์ โดยวิธี Current Divider
 รูปที่ 2.22 แสดงโอห์มมิเตอร์ย่าน Rx10K
รูปที่ 2.22 แสดงโอห์มมิเตอร์ย่าน Rx10K
 รูปที่ 2.23 แสดง Thevenin equivalent circuit ย่าน Rx10K
จากรูปที่ 2.23 ค่า Vth และ Rth หาได้ดังนี้
รูปที่ 2.23 แสดง Thevenin equivalent circuit ย่าน Rx10K
จากรูปที่ 2.23 ค่า Vth และ Rth หาได้ดังนี้
 รูปที่ 2.24 แสดงย่านวัด Rx10K เมื่อวัดค่า Rx ค่า 120KW
จากรูปที่ 2.24 จะได้ว่า
รูปที่ 2.24 แสดงย่านวัด Rx10K เมื่อวัดค่า Rx ค่า 120KW
จากรูปที่ 2.24 จะได้ว่า
 รูปที่ 2.25 แสดงวงจรโอห์มมิเตอร์ที่จะออกแบบ
คำนวณหาคาแรงเคลื่อนเพื่อเลือกใช้แบตเตอรี่ในแต่ละย่านวัด
รูปที่ 2.25 แสดงวงจรโอห์มมิเตอร์ที่จะออกแบบ
คำนวณหาคาแรงเคลื่อนเพื่อเลือกใช้แบตเตอรี่ในแต่ละย่านวัด  รูปที่ 2.26 แสดงวงจรโอห์มมิเตอร์แบบ Potentio-meter ที่ออกแบบ
รูปที่ 2.26 แสดงวงจรโอห์มมิเตอร์แบบ Potentio-meter ที่ออกแบบ